题目内容
17.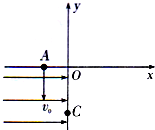 如图所示,在竖直平面内有xOy直角坐标平面,第三象限内存在沿x轴正方向的匀强电场E(大小未知),y轴右侧存在一垂直纸面的匀强磁场,一质量为m、电荷量为q的粒子(不计重力)由A点(-L,0)以一定初速度v0竖直向下抛出,粒子到达y轴上的C点时,其速度方向与y轴负方向夹角为45°,粒子经磁场偏转后从y的正半轴上某点穿出又恰好击中A点.求:
如图所示,在竖直平面内有xOy直角坐标平面,第三象限内存在沿x轴正方向的匀强电场E(大小未知),y轴右侧存在一垂直纸面的匀强磁场,一质量为m、电荷量为q的粒子(不计重力)由A点(-L,0)以一定初速度v0竖直向下抛出,粒子到达y轴上的C点时,其速度方向与y轴负方向夹角为45°,粒子经磁场偏转后从y的正半轴上某点穿出又恰好击中A点.求:(1)电场强度E的大小;
(2)匀强磁场的磁感应强度B的大小;
(3)粒子从A出发到回到A经历的时间t.
分析 (1)带电粒子在电场中做类平抛运动,由类平抛运动的规律可求得电场强度;
(2)由几何关系可明确粒子转动的半径,再由洛仑兹力充当向心力可求得磁感应强度的大小;
(3)明确粒子运动的总过程,分别由类平抛运动、圆周运动及直线运动规律求得各过程中的时间,则可求得总时间.
解答 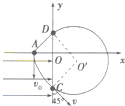 解:(1)带电粒子在电场中做类平抛运动,竖直方向为匀速直线运动,水平方向为匀加速直线运动;
解:(1)带电粒子在电场中做类平抛运动,竖直方向为匀速直线运动,水平方向为匀加速直线运动;
由已知条件可得:
L=$\frac{1}{2}•\frac{qE}{m}{{t}_{1}}^{2}$
OC=v0t1
令粒子在C点的速率为v,有$\frac{qE}{m}{t}_{1}=v$0
v=$\sqrt{2}{v}_{0}$
联立解得:OC=2L,${t}_{1}=\frac{2L}{{v}_{0}}$,$E=\frac{m{{v}_{0}}^{2}}{2qL}$
(2)设粒子在y轴正半轴的D点射出磁场,粒子在磁场中做匀速圆周运动,由左手定则可判定磁场方向垂直纸面向里,
从D点射出时与y轴也成45°角,所以OD=OA=L
可知,CD=$\sqrt{2}r=OC+CD=3L$
r=$\frac{3\sqrt{2}}{2}L$
根据$Bqv=m\frac{v^2}{r}$
解得:B=$\frac{mv}{qr}$
代入得:B=$\frac{2m{v}_{0}}{3qL}$
(3)设粒子在磁场中的运动时间为t2,则${t}_{2}=\frac{270°}{360°}×\frac{2πr}{v}=\frac{9πL}{4{v}_{0}}$
粒子从D到A的运动时间为t3,则${t}_{3}=\frac{DA}{v}=\frac{L}{{v}_{0}}$
所以粒子运动的总时间t=t1+t2+t3=$\frac{12+9π}{{4v}_{0}}L$
答:(1)电场强度E的大小为$\frac{m{{v}_{0}}^{2}}{2qL}$;
(2)匀强磁场的磁感应强度B的大小为$\frac{2m{v}_{0}}{3qL}$;
(3)粒子从A出发到回到A经历的时间t为$\frac{12+9π}{{4v}_{0}}L$.
点评 本题为带电粒子在组合场中的运动,要注意分别应用电场中的类平抛,磁场中的匀速圆周运动的规律进行分析求解.并注意认真分析其对应的物理过程.明确物理规律的正确应用.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | 布朗运动是指在显微镜下观察到的液体分子的无规则运动 | |
| B. | 叶面上的小露珠成球形是液体表面张力的作用 | |
| C. | 不具有规则几何体的物体也可能是晶体 | |
| D. | 氢气和氦气的温度相同时,它们分子的平均速度相同 | |
| E. | 在车胎突然爆裂后的瞬间,车胎内的气体内能减少 |

| A. | 图甲是测定液面高度h的传感器,液面髙度h发生变化时,通过改变两极板之间的正对面积S而引起了电容C的变化 | |
| B. | 图乙是测定压力F的传感器,压力F发生变化时,通过改变两极板之间的正对面积S而引 起了电容C的变化 | |
| C. | 图丙是测定角度θ的传感器,角度θ发生变化时,通过改变两极板之间的正对面积S而引起了电容C的变化 | |
| D. | 三个图都是通过改变两极板之间的距离d而引起电容C的变化 |
 如图所示,轻质弹簧的劲度系数为k,小球所受重力为G,平衡时小球在A处.今用力F竖直向下压小球使弹簧缩短x,让小球静止在B处,则( )
如图所示,轻质弹簧的劲度系数为k,小球所受重力为G,平衡时小球在A处.今用力F竖直向下压小球使弹簧缩短x,让小球静止在B处,则( )| A. | 小球在A处时弹簧的弹力为零 | B. | 小球在A处时弹簧的弹力等于G | ||
| C. | 小球在A处时弹簧的弹性势能较大 | D. | 小球在B处时弹簧的弹性势能较大 |
 有一种电荷控制式喷墨打印机的打印头可以简化成如图所示结构,在墨盒喷出的墨汁微粒经过带电室时被带上负电,带电后的微粒以一定的初速度进入偏转电场,经电场偏转,最后打到白纸上,已知两偏转板长L1=1.6cm,两板间距离d=0.5cm,两板间电压U=8.0×102V,偏转板的右端距离白纸L2=1.6cm,若有一个质量m=1.6×10-11kg、电量q=5.0×10-12C的墨汁微粒,以v0=40m/s的初速度垂直于电场方向进入偏转电场,最后打到正中央O点上方的P点,不计墨汁微粒的重力.
有一种电荷控制式喷墨打印机的打印头可以简化成如图所示结构,在墨盒喷出的墨汁微粒经过带电室时被带上负电,带电后的微粒以一定的初速度进入偏转电场,经电场偏转,最后打到白纸上,已知两偏转板长L1=1.6cm,两板间距离d=0.5cm,两板间电压U=8.0×102V,偏转板的右端距离白纸L2=1.6cm,若有一个质量m=1.6×10-11kg、电量q=5.0×10-12C的墨汁微粒,以v0=40m/s的初速度垂直于电场方向进入偏转电场,最后打到正中央O点上方的P点,不计墨汁微粒的重力. 如图所示是一种折射率n=$\sqrt{2}$的棱镜.现有一束光线沿MN方向射到棱镜的AB面上,入射角的大小i=45°,求:
如图所示是一种折射率n=$\sqrt{2}$的棱镜.现有一束光线沿MN方向射到棱镜的AB面上,入射角的大小i=45°,求: 如图所示,矩形线圈abcd共n=10匝,总电阻为R=10Ω,部分置于有理想边界的匀强磁场中,线圈平面与磁场垂直,磁感应强度大小B=0.5T.线圈ab边长L1=0.4m,ad边长L2=0.5m,在磁场外部分长为$\frac{{2{L_2}}}{5}$,则线圈从图示位置开始以磁场右边界为轴匀速转动,角速度ω=100πrad/s.求:
如图所示,矩形线圈abcd共n=10匝,总电阻为R=10Ω,部分置于有理想边界的匀强磁场中,线圈平面与磁场垂直,磁感应强度大小B=0.5T.线圈ab边长L1=0.4m,ad边长L2=0.5m,在磁场外部分长为$\frac{{2{L_2}}}{5}$,则线圈从图示位置开始以磁场右边界为轴匀速转动,角速度ω=100πrad/s.求: 如图所示,光滑导轨MN和PQ固定在同一水平面上,两导轨距离为L,两端分别接有阻值均为R的定值电阻R1和R2,两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向坚直向下的匀强磁场,磁感应强度为B.一质量为m的金属与与导轨接触良好并静止于ab处,现用一恒力F沿水平方向拉杆,使之由静止起向右运动,若杆出磁场前已做匀速运动,不计导轨及金属杆的电阻.求:
如图所示,光滑导轨MN和PQ固定在同一水平面上,两导轨距离为L,两端分别接有阻值均为R的定值电阻R1和R2,两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向坚直向下的匀强磁场,磁感应强度为B.一质量为m的金属与与导轨接触良好并静止于ab处,现用一恒力F沿水平方向拉杆,使之由静止起向右运动,若杆出磁场前已做匀速运动,不计导轨及金属杆的电阻.求: