题目内容
7. 如图所示,光滑导轨MN和PQ固定在同一水平面上,两导轨距离为L,两端分别接有阻值均为R的定值电阻R1和R2,两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向坚直向下的匀强磁场,磁感应强度为B.一质量为m的金属与与导轨接触良好并静止于ab处,现用一恒力F沿水平方向拉杆,使之由静止起向右运动,若杆出磁场前已做匀速运动,不计导轨及金属杆的电阻.求:
如图所示,光滑导轨MN和PQ固定在同一水平面上,两导轨距离为L,两端分别接有阻值均为R的定值电阻R1和R2,两导轨间有一边长为$\frac{L}{2}$的正方形区域abcd,该区域内有方向坚直向下的匀强磁场,磁感应强度为B.一质量为m的金属与与导轨接触良好并静止于ab处,现用一恒力F沿水平方向拉杆,使之由静止起向右运动,若杆出磁场前已做匀速运动,不计导轨及金属杆的电阻.求:(1)金属杆出磁场前的瞬间流过R1的电流大小和方向;
(2)金属杆做匀速运动时的速率;
(3)金属杆穿过整个磁场过程中R1上产生的电热.
分析 (1)杆出磁场前已做匀速运动,恒力F与安培力平衡,由安培力公式F=BIL和平衡条件求解;
(2)由E=BLv求出感应电动势,由欧姆定律求出电流,然后求出速度v;
(3)金属杆穿过整个磁场过程中,应用能量守恒定律求出电阻产生的热量.
解答 解:(1)设流过金属杆中的电流为I,由平衡条件得:F=BI•$\frac{L}{2}$,解得,I=$\frac{2F}{BL}$,
已知:R1=R2,通过R1的电流:I1=$\frac{I}{2}$=$\frac{F}{BL}$,
根据右手定则判断可知,电流方向从M到P.
(2)设杆做匀速运动的速度为v,
感应电动势:E=Bv•$\frac{L}{2}$,
由欧姆定律得:E=I•$\frac{R}{2}$,
解得:v=$\frac{2FR}{{B}^{2}{L}^{2}}$;
(3)设整个过程电路中产生的总电热为Q,
根据能量守恒定律得:Q=F×$\frac{L}{2}$-$\frac{1}{2}$mv2,
解得:Q=$\frac{1}{2}$FL-$\frac{2m{F}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$,
R1上产生的电热:Q1=$\frac{1}{2}$Q=$\frac{1}{4}$FL-$\frac{m{F}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$;
答:(1)金属杆出磁场前的瞬间流过R1的电流大小为:$\frac{F}{BL}$,方向:从M到P;
(2)金属杆做匀速运动时的速率为$\frac{2FR}{{B}^{2}{L}^{2}}$;
(3)金属杆穿过整个磁场过程中R1上产生的电热为$\frac{1}{4}$FL-$\frac{m{F}^{2}{R}^{2}}{{B}^{4}{L}^{4}}$.
点评 本题是电磁感应与电路、力学相结合的综合题,分析清楚题意,应用E=BLv、欧姆定律、安培力公式、平衡条件、能量守恒定律可以解题.

| A. | 安培力的方向总是垂直于磁场的方向 | |
| B. | 安培力的方向可以不垂直于直导线 | |
| C. | 安培力的大小与通电直导线和磁场方向的夹角无关 | |
| D. | 将直导线从中点折成直角,安培力的大小一定变为原来的一半 |
| A. | 电场强度的方向总是跟电场力的方向一致 | |
| B. | 电场强度的大小总是跟电场力的大小成正比 | |
| C. | 正电荷受到的电场力的方向跟电场强度的方向一致 | |
| D. | 移去检验电荷时,电场强度变为零 |
| A. | 物体做直线运动时路程等于位移的大小 | |
| B. | 路程、速率、时间都是标量 | |
| C. | 加速度的方向与速度的方向一致 | |
| D. | 平均速度的大小等于初、末速度大小的算术平均值 |
 如图是双缝干涉实验装置的示意图,S为单缝,S1、S2为双缝,P为光屏.用绿光从左边照射单缝S时,可在光屏P上观察到干涉条纹.要使相邻条纹间距增大,可以( )
如图是双缝干涉实验装置的示意图,S为单缝,S1、S2为双缝,P为光屏.用绿光从左边照射单缝S时,可在光屏P上观察到干涉条纹.要使相邻条纹间距增大,可以( )| A. | 增大S1与S2的间距 | B. | 减小双缝到光屏的距离 | ||
| C. | 将绿光换为红光 | D. | 将绿光换为紫光 |
| A. | 水平面不光滑时,力F对物体做功的平均功率较大 | |
| B. | 水平面光滑时,力F对物体做功的平均功率较大 | |
| C. | 水平面不光滑时,力F在b点的瞬时功率较大 | |
| D. | 水平面光滑时,力F在b点的瞬时功率较大 |
| A. | a1:a2=1:2 s1:s2=1:2 | B. | a1:a2=1:2 s1:s2=2:1 | ||
| C. | a1:a2=1:2 s1:s2=1:4 | D. | a1:a2=4:1 s1:s2=2:1 |
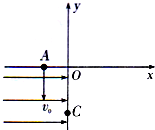 如图所示,在竖直平面内有xOy直角坐标平面,第三象限内存在沿x轴正方向的匀强电场E(大小未知),y轴右侧存在一垂直纸面的匀强磁场,一质量为m、电荷量为q的粒子(不计重力)由A点(-L,0)以一定初速度v0竖直向下抛出,粒子到达y轴上的C点时,其速度方向与y轴负方向夹角为45°,粒子经磁场偏转后从y的正半轴上某点穿出又恰好击中A点.求:
如图所示,在竖直平面内有xOy直角坐标平面,第三象限内存在沿x轴正方向的匀强电场E(大小未知),y轴右侧存在一垂直纸面的匀强磁场,一质量为m、电荷量为q的粒子(不计重力)由A点(-L,0)以一定初速度v0竖直向下抛出,粒子到达y轴上的C点时,其速度方向与y轴负方向夹角为45°,粒子经磁场偏转后从y的正半轴上某点穿出又恰好击中A点.求: