题目内容

【题目】如图所示，水平固定一个光滑长杆，有一个质量为m小滑块A套在细杆上可自由滑动．在水平杆上竖直固定一个挡板P，小滑块靠在挡板的右侧处于静止状态，在小滑块的下端用长为L的细线悬挂一个质量为2m的小球B，将小球拉至左端水平位置使细线处于自然长度，由静止释放，已知重力加速度为g.求：

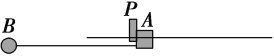
(1)小球运动过程中，相对最低点所能上升的最大高度；

(2)小滑块运动过程中，所能获得的最大速度．

【答案】(1) (2)

【解析】

（1）小球第一次摆到最低点过程中，根据机械能守恒得：2mgL＝(2m)v2，

解得：v=，
小球与小滑块达到共速时，小球上升到最大高度，设此高度为h，根据动量守恒定律得：
2mv=（2m+m）v共
根据能量守恒定律得：(2m)v2＝(3m)v共2+2mgh
解得：h=L
（2）小球摆回最低点时，小滑块获得最大速度，设此时小球速度为v1，滑块的速度为v2，
根据动量守恒定律得：2mv=2mv1+mv2
(2m)v2＝(2m)v12+mv22
解得：v2＝

练习册系列答案
相关题目

【题目】(多选)一横截面为直角三角形的木块按如图所示放置,质量均为的A、B两物体用轻质弹簧相连放在倾角为30°的直角边上,物体C放在倾角为60°的直角边上,B与C之间用跨过定滑轮的轻质细线连接,A、C的质量比为,整个装置处于静止状态。已知物体A、B与斜面间的动摩擦因数相同且最大静摩擦力等于滑动摩擦力,弹簧弹力大小为,C与斜面间无摩擦,则

A. 弹簧处于拉伸状态

B. 物体A所受摩擦力大小为,物体B不受摩擦力作用

C. A、B两物体所受摩擦力大小均为,方向均沿斜面向下

D. 剪断弹簧瞬间,物体A可能下滑

【题目】在“测绘小灯泡的伏安特性曲线”实验中，小灯泡额定电压为2．5V、电流为0．3A。

（1）部分连线的实物照片如图甲所示，请在答题纸上完成实物连接图；

（2）某次实验中，当电流表的示数为0．16A，电压表的指针如图乙所示，则电压为 V， 此时小灯泡的功率是 W；

（3）正确测量获得的伏安特性曲线是下列图象中的 （填字母）。

【题目】在如图所示的装置中，木块B与水平桌面的接触是光滑的，子弹A沿水平方向射入木块后留在木块内，将弹簧压缩到最短。现将子弹、木块和弹簧合在一起作为研究对象（系统），则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中

A. 动量守恒、机械能守恒

B. 动量不守恒、机械能不守恒

C. 动量守恒、机械能不守恒

D. 动量不守恒、机械能守恒

【题目】宇航员在太空站内做了如下实验：选取两个质量分别为mA=0.2kg、mB=0.4kg的小球A、B和一根轻质短弹簧，弹簧的一端与小球A粘连，另一端与小球B接触而不粘连．现使小球A和B之间夹着被压缩的轻质弹簧，处于锁定状态，一起以速度v0=0.1m/s做匀速直线运动，如图所示，过一段时间，突然解除锁定（解除锁定没有机械能损失），两球仍沿原直线运动，从弹簧与小球B刚刚分离开始计时，经时间t=3.0s，两球之间的距离增加了S=2.7m，求弹簧被锁定时的弹性势能Ep．

【题目】对于一定质量的理想气体，当它们的压强和体积发生变化时，下列说法不正确的是（　　）

A. 压强和体积都增大时，其分子平均动能不可能不变

B. 压强和体积都增大时，其分子平均动能有可能减小

C. 压强增大，体积减小时，其分子平均动能有可能不变

D. 压强减小，体积增大时，其分子平均动能有可能增大

【题目】在平直的测试汽车加速性能的场地上，每隔l00m有一个醒目的标志杆，两名测试员驾车由某个标志杆从静止开始匀加速起动，当汽车通过第二个标志杆开始计时，t1=20s时，恰好经过第5个标志杆，t2=40s时，恰好经过第10个标志杆，汽车运动过程中可视为质点，如图所示，求：

(1)汽车的加速度；

(2)若汽车匀加速达到最大速度35m/s后立即保持该速度匀速行驶，则汽车从40s末到60s末经过几个标志杆？

【题目】如图为验证动量守恒定律的实验装置，实验中选取两个半径相同、质量不等的小球，按下面步骤进行实验：

①用天平测出两个小球的质量分别为m1和m2；

②安装实验装置，将斜槽AB固定在桌边，使槽的末端切线水平，再将一斜面BC连接在斜槽末端；

③先不放小球m2,让小球m1从斜槽顶端A处由静止释放，标记小球在斜面上的落点位置P；

④将小球m2放在斜槽末端B处,仍让小球m1从斜槽顶端A处由静止释放,两球发生碰撞,分别标记小球m1、m2在斜面上的落点位置；

⑤用毫米刻度尺测出各落点位置到斜槽末端B的距离。图中从M、P、N点是实验过程中记下的小球在斜面上的三个落点位置,从M、P、N到B点的距离分别为SM、SP、SN.依据上述实验步骤，请回答下面问题：

(1)两小球的质量m1、m2应满足m1___m2(填写“>”、“=”或“<”)；

(2)用实验中测得的数据来表示，只要满足关系式_________________，就能说明两球碰撞前后动量是守恒的；

(3) 若改变两个小球的材质，步骤③中小球m1_______(填写“一定”或“不一定”)落在中间落点位置P；

(4)若两小球的碰撞是弹性碰撞，图中PM分别是小球m1碰前、碰后的落点位置，实验测得BM=15cm，BP=20cm，则小球m2的落点位置BN= ______cm。

【题目】如图所示，为光电计时器的实验简易示意图，当有不透光物体从光电门间通过时， 光电计时器就可以显示物体的挡光时间，实验中所选用的光电门传感器可测的最短时间为0.01ms．光滑水平导轨 MN 上放两个相同物块 A 和 B，其宽度 a =3.0×10-2m，左端挡板处 有一弹射装置 P，右端 N 处与水平传送带平滑连接，今将挡光效果好，宽度为 d ＝3.6×10-3m 的两块黑色磁带分别贴在物块 A 和 B 上，且高出物块，并使高出物块部分在通过光电门时 挡光．传送带水平部分的长度 L =8m，沿逆时针方向以恒定速度 v =6m/s 匀速传动．物块 A、B 与传送带间的动摩擦因数0.2 ，质量 mA =mB =1kg．开始时在 A 和 B 之间压缩一轻弹簧，锁定其处于静止状态，现解除锁定，弹开物块 A 和 B，迅速移去轻弹簧，之后两物块第一次通过光电门，计时器显示读数均为 t =9.0×10-4s． g 取 10m/s2．试求：

（1）弹簧储存的弹性势能 ；

（2）物块 B 沿传送带向右滑动的最远距离 Sm；

（3）物块 B 滑回水平面 MN 的速度大小 ；

（4）若物体 B 返回水平面 MN 后与被弹射装置 P 弹回的物块 A 在水平面上相碰，且 A 和 B 碰后互换速度，则弹射装置 P 至少必须对物块 A 做多少功，才能在 AB 碰后使 B 刚好能 从 Q 端滑出？物块 B 在此滑离皮带的运动过程中，与传送带之间因摩擦产生的内能 ΔE 为 多大？(计算结果可用根号表示)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网