题目内容
5. 如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )
如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )| A. | $\frac{1}{2}$mgR | B. | mgR | C. | 2mgR | D. | $\frac{5}{2}$mgR |
分析 根据牛顿第二定律求出小球通过最低点时的速度,因为小球恰能通过最高点,知最高点的速度为零,根据动能定理求出此过程中小球克服摩擦力所做的功
解答 解:根据牛顿第二定律得,在最低点有:N-mg=m$\frac{{V}^{2}}{R}$,N=6mg,
小球恰好经过最高点,则最高点的速度为0.
根据动能定理得,-mg•2R-Wf=0-$\frac{1}{2}$mV2,
解得:Wf=0.5mgR.
故选:A.
点评 解决本题的关键搞清做圆周运动向心力的来源,运用牛顿第二定律和动能定理进行求解

练习册系列答案
相关题目
16. 如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )
如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )
 如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )
如图是街头变压器通过降压给用户供电的示意图.变压器输入电压是市电网的电压,不会有很大的波动.输出电压通过输电线输送给用户,输电线的电阻用R0表示,变阻器R表示用户用电器的总电阻,当滑动变阻器触头P向下移时( )| A. | 相当于在减少用电器的数目 | |
| B. | A1表的示数随A2表的示数的增大而增大 | |
| C. | V1表的示数随V2表的示数的增大而增大 | |
| D. | 变压器的输入功率在增大 |
20.在圆轨道上运行的质量为m的人造地球卫星,到地面距离等于地球半径,地面处的重力加速度为g,则( )
| A. | 卫星的线速度为$\sqrt{2Rg}$ | B. | 卫星的周期为$4π\sqrt{\frac{2R}{g}}$ | ||
| C. | 卫星的加速度为$\frac{g}{2}$ | D. | 卫星运行的角速度为$\frac{1}{4}\sqrt{\frac{2g}{R}}$ |
10.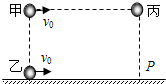 甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )
甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )
 甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )
甲、乙、丙三个小球(均视为质点)分别位于如图所示的竖直平面内,甲、乙在同一条竖直线上,甲、丙在同一条水平线上,与乙在同一水平面上的P点在丙的正下方,在同一时刻甲、乙、丙开始运动,甲以水平速度v0向右平抛,乙以水平速度v0沿水平面向右做匀速直线运动,丙做自由落体运动,不计空气阻力,则( )| A. | 若只有甲、乙两球在水平面上相遇,此时丙球还未着地落到P点 | |
| B. | 无论初速度v0大小如何,甲、乙、丙三球一定不会同时在P点相遇 | |
| C. | 甲、乙、丙三球可能同时相遇在P点 | |
| D. | 若甲、丙两球在空中相遇,此时乙球一定在P点 |
14.用跨过定滑轮的绳把湖中小船拉靠岸,如图所示,已知拉绳的速度v不变,则船速( )


| A. | $\frac{v}{sinθ}$ | B. | $\frac{v}{cosθ}$ | C. | vcosθ | D. | vsinθ |
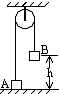 如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少?
如图,跨过光滑的定滑轮的细线两端各系住物体A和B,已知两物体的质量分别是mA=0.1kg,mB=0.3kg,开始时将A用手揿住在地面上,放手后发现A能升起的最大高度为0.9m,问B物体原来离地面的高度h等于多少? 如图所示,一质量为M的塑料球容器放在桌面上,它的内部有劲度系数为k的轻弹簧直立固定与容器的内壁底部,弹簧上端轻绝缘系住一只带正电荷量为q,质量为m的小球,从加上一个向上的匀强电场,场强缓慢增强为E的时候,容器对桌面压力恰好为零,问:
如图所示,一质量为M的塑料球容器放在桌面上,它的内部有劲度系数为k的轻弹簧直立固定与容器的内壁底部,弹簧上端轻绝缘系住一只带正电荷量为q,质量为m的小球,从加上一个向上的匀强电场,场强缓慢增强为E的时候,容器对桌面压力恰好为零,问: 如图所示,水平桌面由粗糙程度不同的AB、BC两部分组成,且AB=BC,小物块P(可视为质点)以某一初速度从A点滑上桌面,最后恰好停在C点,已知物块经过AB与BC两部分的时间之比为1:4,则物块P与桌面上AB、BC部分之间的动摩擦因数μ1、μ2之比为(P物块在AB、BC上所做两段运动可看作匀变速直线运动)( )
如图所示,水平桌面由粗糙程度不同的AB、BC两部分组成,且AB=BC,小物块P(可视为质点)以某一初速度从A点滑上桌面,最后恰好停在C点,已知物块经过AB与BC两部分的时间之比为1:4,则物块P与桌面上AB、BC部分之间的动摩擦因数μ1、μ2之比为(P物块在AB、BC上所做两段运动可看作匀变速直线运动)( )