题目内容
15. 如图所示,水平桌面由粗糙程度不同的AB、BC两部分组成,且AB=BC,小物块P(可视为质点)以某一初速度从A点滑上桌面,最后恰好停在C点,已知物块经过AB与BC两部分的时间之比为1:4,则物块P与桌面上AB、BC部分之间的动摩擦因数μ1、μ2之比为(P物块在AB、BC上所做两段运动可看作匀变速直线运动)( )
如图所示,水平桌面由粗糙程度不同的AB、BC两部分组成,且AB=BC,小物块P(可视为质点)以某一初速度从A点滑上桌面,最后恰好停在C点,已知物块经过AB与BC两部分的时间之比为1:4,则物块P与桌面上AB、BC部分之间的动摩擦因数μ1、μ2之比为(P物块在AB、BC上所做两段运动可看作匀变速直线运动)( )| A. | 1:4 | B. | 1:1 | C. | 8:1 | D. | 4:1 |
分析 设到达B点速度为v1,先根据AB与BC段的位移相等并运用平均速度公式得到B点的速度;然后求解出AB与BC段的加速度,最后根据牛顿第二定律求解出AB、BC部分之间的动摩擦因数μ1、μ2之比.
解答 解:设到达B点速度为v1,由于AB与BC段的位移,有:
$\frac{{v}_{0}+{v}_{1}}{2}•{t}_{1}=\frac{{v}_{1}+0}{2}•{t}_{2}$
其中:t1:t2=1:4
故:${v}_{1}=\frac{{v}_{0}}{3}$
AB段的加速度为:a1=$\frac{{v}_{1}-{v}_{0}}{{t}_{1}}=-\frac{2{v}_{0}}{3{t}_{1}}$
BC段的加速度为:a2=$\frac{0-{v}_{1}}{{t}_{2}}=-\frac{{v}_{0}}{3{t}_{2}}$
根据牛顿第二定律,有:
AB段:-μ1mg=ma1
BC段:-μ2mg=ma2
解得:μ1:μ2=a1:a2=8:1
故选:C.
点评 本题关键是先根据平均速度公式求解出B点速度,得到加速度,然后结合牛顿第二定律列式求解动摩擦因素之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )
如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )
 如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )
如图所示,一内壁粗糙的环形细圆管,位于竖直平面内,环形的半径为R(比细管的直径大得多).在圆管中有一个直径比细管内径略小些的小球(可视为质点),小球的质量为m,设某一时刻小球通过轨道的最低点时对管壁的压力为6mg.此后小球做圆周运动,经过半个圆周恰能过最高点,则此过程中小球克服摩擦力所做的功( )| A. | $\frac{1}{2}$mgR | B. | mgR | C. | 2mgR | D. | $\frac{5}{2}$mgR |
6.如图所示,做简谐运动的水平弹簧振子从平衡位置O向B运动的过程中,下述正确的是( )
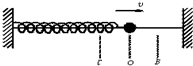

| A. | 振子做匀速运动 | B. | 振子做匀加速运动 | ||
| C. | 振子做加速度不断减小的减速运动 | D. | 振子做加速度不断增大的减速运动 |
3.三个电流表A1、A2、A3分别与电容器、电阻器、电感器串接在一起,接到一电压最大值不变但频率可变的交流电源上,当使交变电流的频率增加时,下列说法正确的是( )
| A. | 三个电流表示数不变 | B. | 三个表的示数都增加 | ||
| C. | A2表的示数变小 | D. | A3表的示数变小 |
10.图甲为某一列沿x轴正向传播的简谐横波在t=1.0s时刻的波形图,图乙为参与波动的某一质点的振动图象,则下列说法不正确的是( )


| A. | 该简谐横波的传播速度为4m/s | |
| B. | 从此时刻起,经过2秒,P质点运动了8米的路程 | |
| C. | 从此时刻起,P质点比Q质点先回到平衡位置 | |
| D. | 乙图可能是甲图x=2m处质点的振动图象 |
7.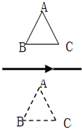 如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )
如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )
 如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )
如图所示,一个闭合三角形导线框ABC位于竖直平面内,其下方(略靠前)固定一根与线框平面平行的水平直导线,导线中通以图示方向的恒定电流.释放线框,它由实线位置下落到虚线位置未发生转动,在此过程中( )| A. | 线框中感应电流方向依次为顺时针→逆时针 | |
| B. | 线框的磁通量为零时,感应电流却不为零 | |
| C. | 线框所受安培力的合力方向依次为向上→向下→向上 | |
| D. | 线框所受安培力的合力为零,做自由落体运动 |
4.把木块放置在水平桌面上,那么下列说法正确的是( )
| A. | 木块对桌面的压力就是重力 | |
| B. | 木块对桌面的压力和木块受到的重力是一对平衡力 | |
| C. | 木块受到的重力和桌面对木块的支持力是一对平衡力 | |
| D. | 木块放在水平桌面上,木块没有发生形变 |
5.如图所示,图甲为某一列简谐横波在t=0.5s 时的波形图,图乙为介质中P处质点的振动图象,则关于该波的说法正确的是( )
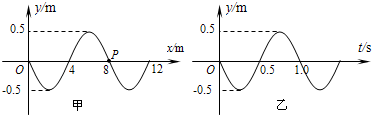

| A. | 传播方向沿+x方向传播 | B. | 波速为16 m/s | ||
| C. | P处质点振动频率为1Hz | D. | P处质点在5s内路程为10 m | ||
| E. | P处质点在5s末内位移为0.5 m |