题目内容
A、B两颗地球卫星绕地球运转的周期之比为2
:1,则( )
| 2 |
分析:人造卫星绕地球做圆周运动受到的万有引力提供向心力,分别用周期、速率来表示向心力,化简公式即可求解结果.
解答:解:A、人造卫星绕地球做圆周运动受到的万有引力提供向心力得,
=
r=
周期之比为T1:T2=2
:1,
则A.B的轨道半径之比为2:1,
根据v=
得线速度之比为1:
,故A正确,B错误
C、由
=ma得
a=
所以向心加速度之比为1:4,故C错误
D、无法判断A、B质量关系,故D错误
故选A.
| GMm |
| r2 |
| m?4π2r |
| T2 |
r=
| 3 |
| ||
周期之比为T1:T2=2
| 2 |
则A.B的轨道半径之比为2:1,
根据v=
| 2πr |
| T |
| 2 |
C、由
| GMm |
| r2 |
a=
| GM |
| r2 |
所以向心加速度之比为1:4,故C错误
D、无法判断A、B质量关系,故D错误
故选A.
点评:对于卫星问题一定掌握:万有引力提供向心力,可以用卫星的速度、周期、角速度来分别表示向心力,从而求出结果.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
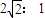 ,则两颗卫星的轨道半径之比为 ,向心加速之比为 .
,则两颗卫星的轨道半径之比为 ,向心加速之比为 .