题目内容
 (2012?南通二模)(选修模块3-4)
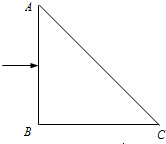
(2012?南通二模)(选修模块3-4)如图所示,等腰直角三角形ABC为一个三棱镜的截面,折射率为n(n>1.5),直角边AB的长为a.一束很细的单色光从AB中点垂直入射,光在真空中的传播速度为c,则该单色光通过三棱镜的时间为多少?
分析:根据v=
求出光在棱镜中的速度,判断出光在AC面上是否发生全反射,结合几何关系求出光在棱镜中走过的路程,求出单色光通过三棱镜的时间.
| c |
| n |
解答:解:设单色光的临界角为C 则sinC=
<
,C<45°.
单色光射入三棱镜后,在AC界面上的入射角i=45°>C,故发生全反射.反射角γ=45°,光垂直于BC边射出,在三棱镜中的路径长度为a.
单色光在三棱镜中的传播速度v=
.
则光通过三棱镜的时间 t=
=
.
答:单色光通过三棱镜的时间为
.
| 1 |
| n |
| 2 |
| 3 |
单色光射入三棱镜后,在AC界面上的入射角i=45°>C,故发生全反射.反射角γ=45°,光垂直于BC边射出,在三棱镜中的路径长度为a.
单色光在三棱镜中的传播速度v=
| c |
| n |
则光通过三棱镜的时间 t=
| a |
| v |
| an |
| c |
答:单色光通过三棱镜的时间为
| an |
| c |
点评:解决本题的关键掌握全反射的条件,掌握光的折射定律,并能灵活运用.

练习册系列答案
相关题目
 (2012?南通二模)如图所示电路中,当电键闭合后,当滑动变阻器滑片P处于中点位置时,小灯泡L1、L2、L3的亮度相同,当滑片P向左滑动时,小灯泡的亮度情况是( )
(2012?南通二模)如图所示电路中,当电键闭合后,当滑动变阻器滑片P处于中点位置时,小灯泡L1、L2、L3的亮度相同,当滑片P向左滑动时,小灯泡的亮度情况是( ) (2012?南通二模)(1)如图甲所示,螺旋测微器读数是
(2012?南通二模)(1)如图甲所示,螺旋测微器读数是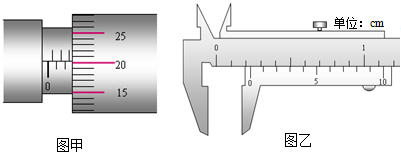
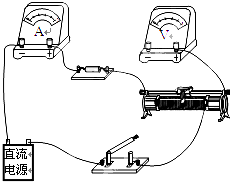 (2012?南通二模)某研究性学习小组为了制作一个传感器,需要选用某种电学元件.实验中首先要描绘该元件的伏安特性曲线,实验室备有下列器材:
(2012?南通二模)某研究性学习小组为了制作一个传感器,需要选用某种电学元件.实验中首先要描绘该元件的伏安特性曲线,实验室备有下列器材: