题目内容
10.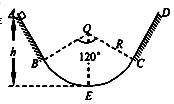 如图所示,在竖直平面内固定一半径R为2m、圆心角为120°的光滑圆弧轨道BEC,其中点E是最低点.在B、C两端平滑、对称地连接AB、CD两段粗糙直轨道,直轨道上端A、D与最低点E之间的高度差h均为2.5m.现将质量为0.01kg的小物块由A点静止释放,物块与直轨道间的动摩擦因数均为0.25.求此后的运动过程中:
如图所示,在竖直平面内固定一半径R为2m、圆心角为120°的光滑圆弧轨道BEC,其中点E是最低点.在B、C两端平滑、对称地连接AB、CD两段粗糙直轨道,直轨道上端A、D与最低点E之间的高度差h均为2.5m.现将质量为0.01kg的小物块由A点静止释放,物块与直轨道间的动摩擦因数均为0.25.求此后的运动过程中:(1)小物块第一次通过E点时的动能大小;
(2)小物块在E点时对轨道压力的最小值;
(3)小物块在直轨道AB和CD上运动的总路程.
分析 (1)对从A到E过程运用动能定理列式求解即可;
(2)最终,滑块在圆弧间来回滑动,根据机械能守恒定律求解E点的最小速度;在E点,重力和支持力的合力提供向心力,根据牛顿第二定律列式求解支持力;
(3)最终,滑块在圆弧间来回滑动,损失的机械能等于摩擦力与AB和CD上运动的总路程的乘积.
解答 解:(1)从A到E过程,有重力和摩擦力做功,根据动能定理,有:
mgh-μmgcos60°•$\frac{h-Rcos60°}{sin60°}$=$\frac{1}{2}m{v}^{2}$
解得:Ek=$\frac{1}{2}m{v}^{2}$=0.23J;
(2)最终,滑块在圆弧间来回滑动,根据机械能守恒定律,有:
mg(R-Rcos60°)=$\frac{1}{2}m{{v}_{E}}^{2}$①
在E点,重力和支持力的合力提供向心力,根据牛顿第二定律,有:
N-mg=m$\frac{{{v}_{E}}^{2}}{R}$②
联立①②解得:
N=0.2N;
(3)最终,滑块在圆弧间来回滑动,由功能关系可知,损失的机械能等于摩擦力与AB和CD上运动的总路程的乘积,所以:
mgh-μmgcosθ•x=mg(R-Rcos60°)
代入数据得:x=3m
答:(1)小物块第一次通过E点时的动能大小为0.23J;
(2)小物块在E点时受到支持力的最小值为0.2N;
(3)小物块在直轨道AB和CD上运动的总路程是12m.
点评 本题关键是明确滑块的运动规律,然后根据动能定理、机械能守恒定律和牛顿第二定律列式求解,解答的过程要明确解答的方向.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.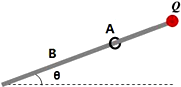 倾角为θ的粗糙绝缘杆顶端固定有一个点电荷Q.在A点无初速度的释放带有恒定电荷,质量为m的小环,小环在Q的电场中沿杆运动到B点静止,杆与小环间的摩擦因数为μ.则从A到B的过程中( )
倾角为θ的粗糙绝缘杆顶端固定有一个点电荷Q.在A点无初速度的释放带有恒定电荷,质量为m的小环,小环在Q的电场中沿杆运动到B点静止,杆与小环间的摩擦因数为μ.则从A到B的过程中( )
 倾角为θ的粗糙绝缘杆顶端固定有一个点电荷Q.在A点无初速度的释放带有恒定电荷,质量为m的小环,小环在Q的电场中沿杆运动到B点静止,杆与小环间的摩擦因数为μ.则从A到B的过程中( )
倾角为θ的粗糙绝缘杆顶端固定有一个点电荷Q.在A点无初速度的释放带有恒定电荷,质量为m的小环,小环在Q的电场中沿杆运动到B点静止,杆与小环间的摩擦因数为μ.则从A到B的过程中( )| A. | 小环速度最大时,小环受到的库仑力为mgsinθ-μmgcosθ | |
| B. | A点的电势一定高于B点的电势 | |
| C. | 小环的电势能可能增加 | |
| D. | 小环克服摩擦力做的功一定大于电势能变化量的大小 |
12. 如图所示,实线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )
如图所示,实线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )
 如图所示,实线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )
如图所示,实线表示某一电场的电场线.在电场力作用下,一带电粒子(不计重力)经A点飞向B点,径迹如图中虚线所示,下列说法正确的是( )| A. | 粒子带正电 | |
| B. | 粒子在A点加速度小 | |
| C. | 粒子在B点动能大 | |
| D. | 带电粒子在B点电势能比在A点的电势能大 |
9.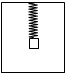 升降机以2m/s2的加速度匀加速上升,某探究小组将质量为0.4kg的物体在升降机中竖直挂在弹簧秤下端,物体同升降机保持相对静止,如图,已知g=10m/s2.下列说法正确的是( )
升降机以2m/s2的加速度匀加速上升,某探究小组将质量为0.4kg的物体在升降机中竖直挂在弹簧秤下端,物体同升降机保持相对静止,如图,已知g=10m/s2.下列说法正确的是( )
 升降机以2m/s2的加速度匀加速上升,某探究小组将质量为0.4kg的物体在升降机中竖直挂在弹簧秤下端,物体同升降机保持相对静止,如图,已知g=10m/s2.下列说法正确的是( )
升降机以2m/s2的加速度匀加速上升,某探究小组将质量为0.4kg的物体在升降机中竖直挂在弹簧秤下端,物体同升降机保持相对静止,如图,已知g=10m/s2.下列说法正确的是( )| A. | 弹簧秤的示数为4 N | B. | 弹簧秤的示数为0.8N | ||
| C. | 物体处于超重状态 | D. | 物体处于失重状态 |
5.关于质点的位移,下列说法正确的是( )
| A. | 位移是标量,只有大小,没有方向 | |
| B. | 位移是矢量,方向从末位置指向初位置 | |
| C. | 位移的正、不负代表大小,只代表方向 | |
| D. | 一个物体的位移为0就没有方向了 |
15.如图甲所示,两平行金属板竖直放置,左极板接地,中间有小孔.右极板电势随时间变化的规律如图乙所示.电子原来静止在左极板小孔处.不计电子的重力,下列说法中正确的是( )
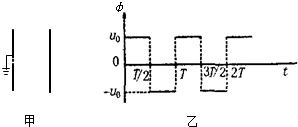

| A. | 从t=0时刻释放电子,电子时而向右运动,时而向左运动,最后打到右极板上 | |
| B. | 从t=0时刻释放电子,电子可能在两板间振动 | |
| C. | 从t=$\frac{T}{4}$时刻释放电子,电子可能在两板间振动,也可能打到右极板上 | |
| D. | 从t=$\frac{3T}{8}$时刻释放电子,电子必将打到右极板上 |
19.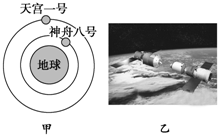 2011年11月3日凌晨1时36分,“天宫一号”目标飞行器与“神舟八号”飞船顺利完成首次交会对接,揭开了中国航天的崭新阶段.假如“神舟八号”与“天宫一号”对接前所处的轨道如图甲所示,图乙是它们在轨道上即将对接时的模拟图.当它们处于图甲所示的轨道运行时,下列说法正确的是( )
2011年11月3日凌晨1时36分,“天宫一号”目标飞行器与“神舟八号”飞船顺利完成首次交会对接,揭开了中国航天的崭新阶段.假如“神舟八号”与“天宫一号”对接前所处的轨道如图甲所示,图乙是它们在轨道上即将对接时的模拟图.当它们处于图甲所示的轨道运行时,下列说法正确的是( )
 2011年11月3日凌晨1时36分,“天宫一号”目标飞行器与“神舟八号”飞船顺利完成首次交会对接,揭开了中国航天的崭新阶段.假如“神舟八号”与“天宫一号”对接前所处的轨道如图甲所示,图乙是它们在轨道上即将对接时的模拟图.当它们处于图甲所示的轨道运行时,下列说法正确的是( )
2011年11月3日凌晨1时36分,“天宫一号”目标飞行器与“神舟八号”飞船顺利完成首次交会对接,揭开了中国航天的崭新阶段.假如“神舟八号”与“天宫一号”对接前所处的轨道如图甲所示,图乙是它们在轨道上即将对接时的模拟图.当它们处于图甲所示的轨道运行时,下列说法正确的是( )| A. | “神舟八号”的运行速度比“天宫一号”的小 | |
| B. | “神舟八号”的运行周期比“天宫一号”的长 | |
| C. | “神舟八号”适度加速后有可能与“天宫一号”实现对接 | |
| D. | 航天员在天宫一号中处于失重状态,说明航天员不受地球引力作用 |
20.下列关于功的说法中,正确的是( )
| A. | 静摩擦力总是不做功 | |
| B. | 滑动摩擦力总是做负功 | |
| C. | 凡是既受力又发生位移的物体,一定有力对物体做功 | |
| D. | 物体在运动过程中,若所受力的方向总是垂直于速度的方向,此力不做功 |
