��Ŀ����
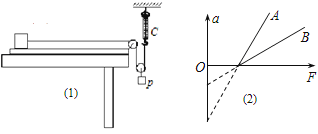
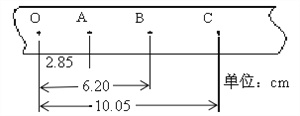
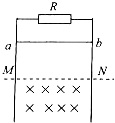
����Ŀ��ͼʾ�Ļ�״���������ֱ���ڣ����ɰ뾶�ֱ�ΪR��2R��������Բ������뾶ΪR�������ķ�֮һԲ������������ȷֱ�Ϊ2R��4R��ֱ���ƽ�����Ӷ��ɣ���ˮƽ��MN��PQΪ�磬�ռ��Ϊ������������I��������дŸ�Ӧǿ��ΪB��ˮƽ�������ǿ�ų�������I�͢�����ֱ���ϵ���ǿ�糡��һ����Ϊm�������Ϊ+q�Ĵ���С�����ڹ���ڣ���������ֱ�����Ķ�Ħ������Ϊ�̣�0���̣�1�����������Բ���β��־��⻬���ڵ糡�п���C��ĵط���С�������ͷţ���С���������ֲ��䣨��֪����I��II����ǿ�糡ǿ��СΪE= ![]() ���������ٶ�Ϊg������
���������ٶ�Ϊg������
��1��С�����ͷ�ʱ���ٶ�aC�Ĵ�С
��2��С����һ��ͨ�������ߵ�Aʱ�ܵ������ѹ��N�Ĵ�С
��3������C���ͷ�С����ͬʱ��������II������һ��ֱ�ڹ��ƽ�������ˮƽ��ǿ�糡���䳡ǿ��СΪE��= ![]() ������С��������ֱ�����ͨ������·��s�� ��
������С��������ֱ�����ͨ������·��s�� ��
���𰸡�
��1���⣺��С����C�㣬��ţ�ٵڶ����ɵã�
qE��mg=mac��
��ã�ac=g��
��С�����ͷ�ʱ���ٶ�aC�Ĵ�СΪg��
��2���⣺��C��A������������������С���Թ����ѹ����Ҳ�Ͳ��ܹ����Ħ�������ɶ��ܶ����ã�
qE5R��mg5R= ![]() mvA2��0��
mvA2��0��
С����A��ʱ����ţ�ٵڶ����ɵã�
F+mg��qvAB��qE=m ![]() ��
��
��ã�F=11mg+qB ![]() ��
��
��С����һ��ͨ�������ߵ�Aʱ�ܵ������ѹ��N�Ĵ�СΪ11mg+qB ![]() ��
��
��3���⣺����0���̣�1��С������ͨ��A�㣬�Ժ��ж��ֿ��ܣ�
�ٿ���ǡ��ͣ��K�㣬�������˶����̣��ɶ��ܶ�����
qE3R��mg3R����qE��s��=0��
��ã�s��= ![]() ��
��
�ڻ�����������D��D����ٶ�Ϊ�㣨����D��D���֮�������˶������ɶ��ܶ����ã�
qE4R��mg4R����qE��s��=0��
��ã�s��= ![]() ��
��
������C���ͷ�С����ͬʱ��������II������һ��ֱ�ڹ��ƽ�������ˮƽ��ǿ�糡���䳡ǿ��СΪE��= ![]() ��С��������ֱ�����ͨ������·��s��Ϊ
��С��������ֱ�����ͨ������·��s��Ϊ ![]() ��
�� ![]() ��
��
����������1����ţ�ٵڶ����ɿ���������ٶȣ���2���ɶ��ܶ���������ٶȣ���ţ�ٵڶ��������ѹ������3��Ӧ�ö��ܶ����������·�̣�