Question

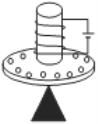
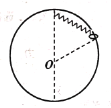
【题目】如图所示，一轻弹簧一端固定在竖直放置光滑大圆环最高点，大圆环半径为R，另一端栓接一轻质小圆环，小圆环套在大圆环上，开始时弹簧与竖直方向成60°，当在小圆环上挂一质量为m的物体后使之缓慢下降，静止时弹簧与竖直方向成45°。求：

(1)弹簧的劲度系数；

(2)当在小圆环上挂多大质量的物体，静止时弹簧与竖直方向成37°；

(3)当在小圆环上挂的质量满足什么条件时，稳定后，小圆环处于最低位置。（弹簧始终在弹性限度内，sin37°=0.6，cos37°=0.8）

Answer 1

【答案】(1)； (2)； (3)

【解析】

(1)静止时弹簧与竖直方向成45°，对圆环进行受力分析，如图所示：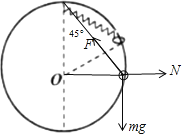

根据平衡条件，弹簧的弹力

根据几何关系，弹簧的伸长量

△x=（-1）R

根据胡克定律

F=k△x

联合上面各式解得

(2)设静止时弹簧与竖直方向成θ，小环上挂的物体的质量为m1，对圆环进行受力分析，受到重力m1g、弹簧的拉力F、大圆环的支持力N，根据平衡条件，作出三个力的矢量三角形，如图所示：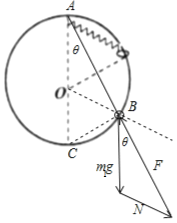

根据几何知识，力的矢量三角形和实物三角形AOB相似，而OA和OB都等于R，所以m1g和N始终相等

AB=2Rcosθ

F=2m1gcosθ

弹簧的伸长量

△x=2Rcosθ-R=（2cosθ-1）R

根据胡克定律

F=k△x

即

①

当θ=37°时，代入①式解得

(3)小圆环恰好处于最低位置，此时θ=0，代入①式解得

所以小圆环所挂物体质量时，小圆环可以处于最低点。