题目内容
【题目】如图所示,是一个半径为R的半圆柱形透明物体的截面图。现有平行于轴线OA的单色光从左侧射入透明物体,已知从距圆心![]() 的P点射入透明物体的光,经过透明物体后通过轴线OA上的Q点,Q点距圆心O的距离为
的P点射入透明物体的光,经过透明物体后通过轴线OA上的Q点,Q点距圆心O的距离为![]() 。求:
。求:

(1)该透明物体的折射率;
(2)能够从透明物体圆形边界射出的光(不考虑多次反射的情况),其入射光的范围。
【答案】(1) ![]() (2) 入射光的范围在距O点小于
(2) 入射光的范围在距O点小于![]() 的距离内
的距离内
【解析】
(i) 如图,
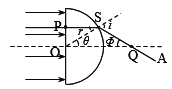
设光在弧面上的入射点为S,入射角为r,折射角为i,OS与OA夹角为![]() ,由几何关系:
,由几何关系:
![]()
设S、Q间的距离分别为![]() ,
,
由题意可得O、Q间距:![]()
在![]() OSQ中,由余弦定理得:
OSQ中,由余弦定理得:![]()
代入数据得:![]()
![]() OSQ为等腰三角形
OSQ为等腰三角形
设SQ与OA的夹角为Φ,
由几何知识可得:Φ =θ,i=Φ +θ
由折射定律:![]()
代入数据得:![]()
(ii)设临界角为C,入射光离O的最远距离为d,由折射定律:![]()
根据几何关系:![]()
代入数据得:![]() ,即入射光的范围在距O点小于
,即入射光的范围在距O点小于![]() 的距离内。
的距离内。

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目