题目内容
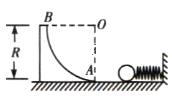
【题目】如图所示,质量为M = 1.0 kg的光滑![]() 弧形槽AB静止在光滑的水平地面上,其半径为R = 0.7m,弧形槽过B点的切线竖直,用质量为m = 1.0 kg的小球将弹簧压缩在竖直墙上并锁定,弹簧储存的弹性势能为50 J。解除锁定后,小球脱离弹簧冲上弧形槽,并能从弧形槽的最高点B冲出,重力加速度g= 10 m/s2,小球可视为质点,忽略空气阻力。求:
弧形槽AB静止在光滑的水平地面上,其半径为R = 0.7m,弧形槽过B点的切线竖直,用质量为m = 1.0 kg的小球将弹簧压缩在竖直墙上并锁定,弹簧储存的弹性势能为50 J。解除锁定后,小球脱离弹簧冲上弧形槽,并能从弧形槽的最高点B冲出,重力加速度g= 10 m/s2,小球可视为质点,忽略空气阻力。求:
(1)小球冲出弧形槽最高点后做什么运动,上升的最大高度为多少;
(2)小球落回弧形槽后,与弧形槽分离,滑上水平地面时的速度是多少;
(3)小球从冲出B点到再次落回到弧形槽时,弧形槽向前运动了多长。
【答案】(1)斜上抛运动;1.8m;(2)0;(3)6m
【解析】
(1)设解除锁定后,小球获得的速度为v0,由能量守恒得
![]()
当小球冲出槽的最高点时,两者在水平方向共速,设此时小球水平速度为vx,竖直速度为vy,由水平方向动量守恒和机械能守恒得
![]()
![]()
联立解得
![]() ,
,![]()
所以小球相对于斜槽做竖直上抛运动,相对于地面做斜上抛运动。
设小球上升的最大高度为h,则
![]()
解得
![]()
(2)小球落回弧形槽后,与弧形槽分离,滑上水平地面时,设小球和圆弧槽的速度分别为v1和v2,取水平向右为正方向,由系统水平方向动量守恒和机械能守恒得
![]()
![]()
联立代入数据解得
![]() ,
,![]()
故小球落回弧形槽后,与弧形槽分离,滑上水平地面时的速度为0。
(3)由![]() 得
得

所以小球在空中运动的总时间为
![]()
小球从冲出B点到再次落回到弧形槽时,弧形槽向前运动的距离为
![]()

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目








