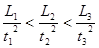题目内容
将甲乙两小球先后以同样的速度在距地面不同高度处竖直向上抛出,抛出时间相隔2 s,它们运动的图像分别如直线甲乙所示。则
| A.t=2 s时,两球的高度相差一定为40 m |
| B.t=4 s时,两球相对于各自的抛出点的位移相等 |
| C.两球从抛出至落到地面所用的时间间隔相等 |
| D.甲球从抛出至到达最高点的时间间隔与乙球相等 |
BD
解析试题分析:根据速度时间图象与时间轴所围的“面积”表示质点的位移,知t=2s时,甲球通过的位移为
x甲=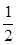 ×(30+10)×2m=40m,乙的位移为零,两球位移之差等于40m,但两球初始的高度未知,故t=2s时两球的高度相差不一定为40m.故A错误.t=4s时,甲球相对于抛出点的位移为
×(30+10)×2m=40m,乙的位移为零,两球位移之差等于40m,但两球初始的高度未知,故t=2s时两球的高度相差不一定为40m.故A错误.t=4s时,甲球相对于抛出点的位移为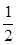 ×30×3-
×30×3-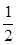 ×10×1=40m,乙球相对于抛出点的位移为
×10×1=40m,乙球相对于抛出点的位移为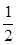 ×(30+10)×2m=40m,故两球相对于各自的抛出点的位移相等.故B正确.
×(30+10)×2m=40m,故两球相对于各自的抛出点的位移相等.故B正确.
两球从不同的高度以同样的速度竖直向上抛出,根据竖直上抛运动的规律x=-h=v0t-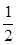 gt2,h是抛出点距地面的高度,可知两球从抛出至落到地面所用的时间间隔t不相等.故C错误.由图知,甲球从抛出至到达最高点的时间间隔与乙球相等,都是3s.故D正确.故选BD.
gt2,h是抛出点距地面的高度,可知两球从抛出至落到地面所用的时间间隔t不相等.故C错误.由图知,甲球从抛出至到达最高点的时间间隔与乙球相等,都是3s.故D正确.故选BD.
考点:匀变速运动的规律。

某航母跑道长200m。飞机在航母上滑行的最大加速度为6m/s2,起飞需要的最低速度为50m/s,那么,飞机在滑行前,需要借助弹射系统获得的最小初速度为( )
| A.5m/s | B.10m/s | C.15m/s | D.20m/s |
一物体在外力的作用下从静止开始做直线运动,合外力方向不变,大小随时间的变化如图所示。设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2,速度分别是v1和v2,合外力从开始至t0时刻做的功是W1,从t0至2t0时刻做的功是W2,则( )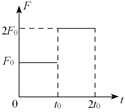
| A.x2 = 5x1 v2 = 3v1 | B.x1 = 9x2 v2 = 5v1 |
| C.x2 = 5x1 W2 = 8W1 | D.v2 = 3v1 W2 = 9W1 |
如图所示,竖直平面内的轨道Ⅰ和Ⅱ都由两段细直杆连接而成,两轨道长度相等。用相同的水平恒力将穿在轨道最低点的B静止小球,分别沿Ⅰ和Ⅱ推至最高点A,所需时间分别为t1、t2;动能增量分别为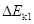 、
、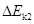 。假定球在经过轨道转折点前后速度的大小不变,且球与Ⅰ、Ⅱ轨道间的动摩擦因数相等,则
。假定球在经过轨道转折点前后速度的大小不变,且球与Ⅰ、Ⅱ轨道间的动摩擦因数相等,则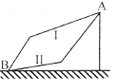
A.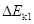 > >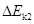 ;t1>t2 ;t1>t2 | B.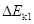 = =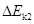 ;t1>t2 ;t1>t2 |
C.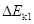 > >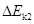 ;t1<t2 ;t1<t2 | D.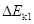 = =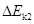 ;t1<t2 ;t1<t2 |
若以固定点为起点画若干矢量,分别代表质点在不同时刻的速度,则这些矢量的末端所形成的轨迹被定义为“速矢端迹”。由此可知下列说法正确的是:
| A.匀速直线运动的速矢端是点 | B.匀加速直线运动的速矢端是射线 |
| C.平抛运动的速矢端是抛物线 | D.匀速圆周运动的速矢端迹是圆 |
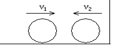
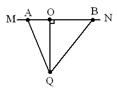

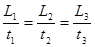 B.
B.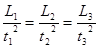
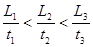 D.
D.