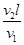题目内容
潜艇部队经常开展鱼雷攻击敌方舰艇演练。某次演习的简化模型为:敌舰沿直线MN匀速航行,潜艇隐蔽在Q点不动,Q到MN的距离QO="2000" m。当敌舰到达距离O点800 m的A点时,潜艇沿QO方向发射一枚鱼雷,正好在O点击中敌舰。敌舰因受鱼雷攻击,速度突然减为原来的一半,且立刻沿原运动方向做匀加速运动逃逸。100s后潜艇沿QB方向发射第二枚鱼雷,鱼雷在B点再次击中敌舰。测得OB="1500" m,不考虑海水速度的影响,潜艇和敌舰可视为质点,鱼雷的速度大小恒为25 m/s。求: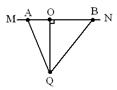
(1)敌舰第一次被击中前的速度;
(2)鱼雷由Q至B经历的时间;
(3)敌舰逃逸时的加速度大小。
(1)10m/s(2)100s(3)0.025s
解析试题分析:(1)鱼雷从Q到O经历的时间
t1=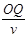 =
=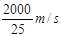 =80s
=80s
敌舰被击中前的速度v1=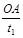 =
=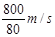 =10m/s
=10m/s
(2)设第二枚鱼雷经过时间t2击中敌舰,则
QB=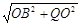 =2500m
=2500m
t2=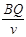 =
=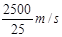 =100s
=100s
(3)敌舰第一次被击中后瞬间的速度v2=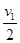 =5m/s
=5m/s
敌舰被第一次击中后运动的时间t3=t2+100s=200s
设敌舰的加速度为a,由OB=v2t3+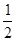 at32
at32
得a=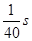 =0.025s
=0.025s
考点:此题考查匀速直线运动及匀变速直线运动的规律。

如图所示,轮子的半径均为R=0.20 m,且均由电动机驱动以角速度ω=8.0 rad/s逆时针匀速转动,轮子的转动轴在同一水平面上,轴心相距d=1.6 m.现将一块均匀木板轻轻地平放在轮子上,开始时木板的重心恰好在O2轮的正上方,已知木板的长度L>2d,木板与轮子间的动摩擦因数均为μ=0.16,则木板的重心恰好运动到O1轮正上方所需要的时间是( )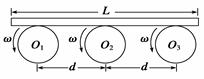
| A.1 s | B.0.5 s |
| C.1.5 s | D.条件不足,无法判断 |
在交通事故的分析中,刹车线的长度是很重要的依据,刹车线是汽车刹车后,停止转动的轮胎在地面上发生滑动时留下的滑动痕迹.在某次交通事故中,汽车的刹车线长度是14 m,假设汽车轮胎与地面间的动摩擦因数恒为0.7,g取10 m/s2,则汽车刹车前的速度大小为( )
| A.7 m/s | B.10 m/s | C.14 m/s | D.20 m/s |
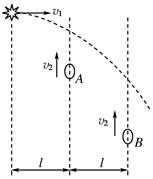
将甲乙两小球先后以同样的速度在距地面不同高度处竖直向上抛出,抛出时间相隔2 s,它们运动的图像分别如直线甲乙所示。则
| A.t=2 s时,两球的高度相差一定为40 m |
| B.t=4 s时,两球相对于各自的抛出点的位移相等 |
| C.两球从抛出至落到地面所用的时间间隔相等 |
| D.甲球从抛出至到达最高点的时间间隔与乙球相等 |
 从地面由静止开始竖直向上起飞,已知飞机在上升过程中每秒钟的耗油量V=
从地面由静止开始竖直向上起飞,已知飞机在上升过程中每秒钟的耗油量V= (p,q均为常数),若直升飞机欲加速上升到某一高度处,且耗油量最小,则其加速度大小应为( )
(p,q均为常数),若直升飞机欲加速上升到某一高度处,且耗油量最小,则其加速度大小应为( )




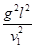
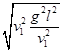
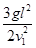 +
+