题目内容
(14分)如图所示,固定的光滑平台上固定有光滑的半圆轨道,轨道半径R=0.6m。平台上静止着两个滑块A、B,mA=0.1Kg,mB=0.2Kg,两滑块间夹有少量炸药,平台右侧有一带挡板的小车,静止在光滑的水平地面上。小车质量为M=0.3Kg,车面与平台的台面等高,车面左侧粗糙部分长度为L=0.8m,动摩擦因数为μ=0.2,右侧拴接一轻质弹簧,弹簧自然长度所在处车面光滑。点燃炸药后,A滑块到达轨道最高点时对轨道的压力大小恰好等于A滑块的重力,滑块B冲上小车。两滑块都可以看作质点,炸药的质量忽略不计,爆炸的时间极短,爆炸后两个物块的速度方向在同一水平直线上,且g=10m/s2。

求:(1)滑块在半圆轨道最低点对轨道的压力
(2)炸药爆炸后滑块B的速度大小
(3)滑块B滑上小车后的运动过程中弹簧的最大弹性势能

求:(1)滑块在半圆轨道最低点对轨道的压力
(2)炸药爆炸后滑块B的速度大小
(3)滑块B滑上小车后的运动过程中弹簧的最大弹性势能
(1)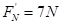 (2)
(2) (3)
(3)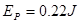
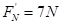 (2)
(2) (3)
(3)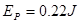
试题分析:(1)在最高点由牛顿第二定律:
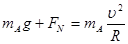 ……(1分)
……(1分)由已知最高点压力
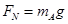
由机械能守恒定律:
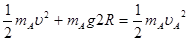 …………(2分)
…………(2分)在半圆轨道最低点由牛顿第二定律:
 …………(1分)
…………(1分)解得:
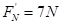 …………(1分)
…………(1分)由牛顿第三定律:
滑块在半圆轨道最低点对轨道的压力大小为7N,方向竖直向下 ……(1分)
(2)由动量守恒定律:
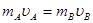 …………(2分)
…………(2分)  …………(1分)
…………(1分)(3)由动量守恒定律:
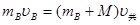 …………(1分)
…………(1分)由能量守恒定律:
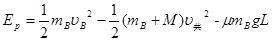 …………(3分)
…………(3分)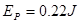 ………… (1分)
………… (1分)点评:做此类型的题目,关键是弄清楚物体不同时间段内的运动性质,然后选择对应的规律分析解题

练习册系列答案
相关题目



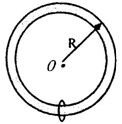
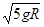
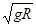

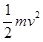
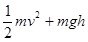
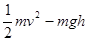
 的圆弧轨道,O为圆心,OA水平,OB竖直,一小球从A点沿轨道射入,速度是v1,小球到达最高点B的速度是v2,则v1与v2比值可能是( )
的圆弧轨道,O为圆心,OA水平,OB竖直,一小球从A点沿轨道射入,速度是v1,小球到达最高点B的速度是v2,则v1与v2比值可能是( )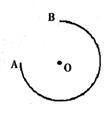
 : 1
: 1