题目内容
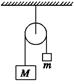
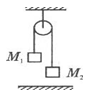
如图所示，一很长的、不可伸长的柔软轻绳跨过光滑定滑轮，绳两端各系一小球
a和b。a球质量为2m，静置于地面；b球质量为3m，用手托住，高度为h，此时轻绳刚好拉紧．从静止开始释放b后，求a可达到的最大高度.
a和b。a球质量为2m，静置于地面；b球质量为3m，用手托住，高度为h，此时轻绳刚好拉紧．从静止开始释放b后，求a可达到的最大高度.
1.2h
试题分析：在b球落地前，a．b球组成的系统机械能守恒，且a．b两球速度大小相等，设为v，根据机械能守恒定律有：3mgh－2mgh＝
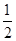(2m＋3m)v2，解得：
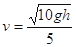
b球落地时，a球高度为h，之后a球向上做竖直上抛运动，由机械能守恒有，
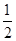(2m)v2＝2mgΔhΔh＝＝0.2h
所以a球可能达到的最大高度为H=h+0.2h=1.2h．
点评：在a球上升的全过程中，a球的机械能是不守恒的，所以在本题中要分过程来求解，第一个过程系统的机械能守恒，在第二个过程中只有a球的机械能守恒．
练习册系列答案
相关题目
m/s
，场强大小为E＝
，取重力加速度g＝10m/s2，不计空气阻力，小物块电荷量不变，求：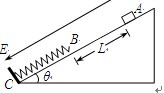
时对纸带上起点的要求是 ，为此目的，所选择的纸带第１，２两点间距应接近 ．
＝ ，重锤动能
＝ ．从开始下落起至Ｂ点，重锤的重力势能减少量是ΔEP＝ ，因此可以得出的结论是 ．（g="10" m/s2）
为纵轴，以ｈ为横轴画出的图线应是下图中的（ ）
