题目内容
【题目】如图,固定斜面的顶端安装一定滑轮,左倾角α=53°,右斜面倾角θ=37°,一轻绳跨过定滑轮,两端分别与小物块P和质量为M的小物块Q连接.初始时刻两物块恰好处于静止状态,且离水平地面高度均为h,一切摩擦均不计,P、Q均可视为质点,重力加速度大小为g,取sin37°=0.6,sin53°=0.8.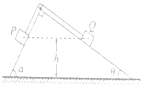
(1)物块P、Q的质量之比为多大?
(2)若将轻绳剪断后,之后两物块沿各自斜面下滑,求P、Q在斜面上运动的时间之比;
(3)若用手按住Q不动,P的质量增加为原来的2倍,Q的质量为M,放手后,Q不会触及滑轮,P着地后将轻绳子剪断,求放手后Q运动到最高点所经历的时间t.
【答案】
(1)解:设P的质量为m.轻绳剪断前,两物块受力平衡,有:
mgsinα=Mgsinθ
得物块P、Q的质量之比为:
![]() =
= ![]() =
= ![]()
答:物块P、Q的质量之比为3:4;
(2)解:轻绳剪断后,两物块在各自斜面上做初速度为零的匀加速直线运动,设P、Q在斜面上运动的时间分别为t1、t2,加速度分别为a1、a2,则:
![]() =
= ![]() a1t12
a1t12
![]() =
= ![]() a2t22
a2t22
根据牛顿第二定律有:
a1= ![]() =gsinα
=gsinα
a2= ![]() =gsinθ
=gsinθ
得: ![]() =
= ![]() =
= ![]()
答:若将轻绳剪断后,之后两物块沿各自斜面下滑,P、Q在斜面上运动的时间之比为3:4;
(3)解:放手后,P沿斜面向下运动,Q先沿斜面向上运动,根据牛顿第二定律,对P,有:
2mgsinα﹣T=2ma
对Q,有:
T﹣Mgsinθ=Ma
解得:
a= ![]() g
g
对Q有:
υ2=2a ![]()
得:υ= ![]()
而υ=at3,υ=a2t4
得:t=t3+t4= ![]() =
= ![]()
答:放手后Q运动到最高点所经历的时间t为 ![]() .
.
【解析】(1)两物块受力平衡,各自的重力平行斜面方向的分力相等;
(2)先根据牛顿第二定律求解加速度之比,再根据位移公式求解时间之比;
(3)对两个物体分别受力分析,根据牛顿第二定律列式求解加速度,然后根据运动学公式列式求解