题目内容
如图所示,有一质量M="2" kg的平板小车静止在光滑水平面上,小物块A 、B 静止在板上的C 点,A 、B间绝缘且夹有少量炸药。已知mA=2 kg,mB=1kg,A 、B 与小车间的动摩擦因数均为μ=0.2。A 带负电,电量为q , B 不带电。平板车所在区域有范围很大的、垂直纸面向里的匀强磁场,磁感应强度为B,且电荷量与磁感应强度q.B="10" N·s / m .炸药瞬间爆炸后释放的能量为12 J,并全部转化为A 、B的动能,使得A 向左运动,B 向右运动.取g=10 m/s2,小车足够长,求:

(1)分析说明爆炸后AB的运动情况(请描述加速度、速度的变化情况)
(2)B在小车上滑行的距离。

(1)分析说明爆炸后AB的运动情况(请描述加速度、速度的变化情况)
(2)B在小车上滑行的距离。
(1)vA=2m/s,vB=4m/s(2)Δs=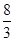 m
m
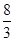 m
m解:(运动描述2分)炸开瞬间,对A、B有:
0=mAvA-mBvB ① (1分)
E=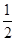 mAvA2+
mAvA2+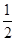 mBvB2 ② (1分)
mBvB2 ② (1分)
解得:vA=2m/s,vB=4m/s (1分)
爆炸后对A有:
qBvA=mAg ③
因此,A与车之间无摩擦力而做匀速运动,从左端滑离小车,对B与小车组成的系统有:
mBvB=(mB+M)v ④ (1分)
-μmBgΔs =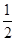 (M+mB)v2-
(M+mB)v2-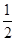 mBvB2 ⑤ (2分)
mBvB2 ⑤ (2分)
解得:Δs=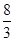 m ⑥ (1分)
m ⑥ (1分)
0=mAvA-mBvB ① (1分)
E=
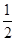 mAvA2+
mAvA2+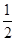 mBvB2 ② (1分)
mBvB2 ② (1分)解得:vA=2m/s,vB=4m/s (1分)
爆炸后对A有:
qBvA=mAg ③
因此,A与车之间无摩擦力而做匀速运动,从左端滑离小车,对B与小车组成的系统有:
mBvB=(mB+M)v ④ (1分)
-μmBgΔs =
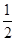 (M+mB)v2-
(M+mB)v2-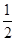 mBvB2 ⑤ (2分)
mBvB2 ⑤ (2分)解得:Δs=
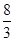 m ⑥ (1分)
m ⑥ (1分)
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目


 ,滑块CD上表面是光滑的1/4圆弧,其始端D点切线水平且在木板AB上表面内,它们紧靠在一起,如图所示.一可视为质点的物块P,质量也为m,从木板AB的右端以初速度v0滑上木板AB,过B点时速度为v0/2,又滑上滑块CD,最终恰好能滑到滑块CD圆弧的最高点C处,求:
,滑块CD上表面是光滑的1/4圆弧,其始端D点切线水平且在木板AB上表面内,它们紧靠在一起,如图所示.一可视为质点的物块P,质量也为m,从木板AB的右端以初速度v0滑上木板AB,过B点时速度为v0/2,又滑上滑块CD,最终恰好能滑到滑块CD圆弧的最高点C处,求:




