题目内容
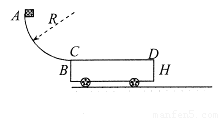
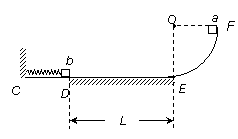
如图所示,光滑的![]() 圆弧轨道固定在竖直平面内,与水平轨道CE连接。水平轨道的CD段光滑、DE段粗糙。一根轻质弹簧一端固定在C处的竖直面上,另一端与质量为2m的物块b刚好在D点接触(不连接),弹簧处于自然长度。将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑。物块a与物块b第一次碰撞后一起向左压缩弹簧。
圆弧轨道固定在竖直平面内,与水平轨道CE连接。水平轨道的CD段光滑、DE段粗糙。一根轻质弹簧一端固定在C处的竖直面上,另一端与质量为2m的物块b刚好在D点接触(不连接),弹簧处于自然长度。将质量为m的物块a从顶端F点静止释放后,沿圆弧轨道下滑。物块a与物块b第一次碰撞后一起向左压缩弹簧。
已知圆弧轨道半径为r,![]() =L,物块a、b与DE段水平轨道的动摩擦因数分别为μ1=0.2和μ2=0.4,重力加速度为g。物块a、b均可视为质点。求:
=L,物块a、b与DE段水平轨道的动摩擦因数分别为μ1=0.2和μ2=0.4,重力加速度为g。物块a、b均可视为质点。求:
(1)物块a第一次经过E点时的速度是多少?
(2)试讨论L取何值时,a、b能且只能发生一次碰撞?
解:(1)物块a由F到E过程中,由机械能守恒有: ![]() ……(2分)
……(2分)
解得第一次经过E点时的速度 ![]() ………………………………(2分)
………………………………(2分)
(2)物块a从E滑至D过程中,由动能定理有:
![]() ………………………………………………(2分)
………………………………………………(2分)
解得物块a在D点时的速度 ![]()
![]() ……………………(1分)
……………………(1分)
物块a、b在D点碰撞,根据动量守恒有:![]() ……………(2分)
……………(2分)
解得两物块在D点向左运动的速度![]() ………………(1分)
………………(1分)
a、b一起压缩弹簧后又返回D点时速度大小![]() ……(1分)
……(1分)
由于物块b的加速度大于物块a的加速度,所以经过D后,a、b两物块分离,同
时也与弹簧分离。
讨论:① 假设a在D点时的速度![]() 0,即 l = 5r …………………………(1分)
0,即 l = 5r …………………………(1分)
要使a、b能够发生碰撞,则l < 5r……………………………………(2分)
② 假设物块a滑上圆弧轨道又返回,最终停在水平轨道上P点,物块b在水平轨道上匀减速
滑至P点也恰好停止,设![]() ,则
,则![]() ,根据能量守恒,
,根据能量守恒,
对a物块 ![]() …………………………………………(1分)
…………………………………………(1分)
对b物块 ![]() ………………………………………(1分)
………………………………………(1分)
由以上两式解得 ![]() ………………………………………(1分)
………………………………………(1分)
将![]() 代入
代入 ![]()
解得 ![]() ……………………………………………………………………(1分)
……………………………………………………………………(1分)
要使a、b只发生一次碰撞,则![]() …………………………………………(1分)
…………………………………………(1分)
综上所述,当![]() 时,a、b两物块能且只能发生一次碰撞………………(1分)
时,a、b两物块能且只能发生一次碰撞………………(1分)

 阅读快车系列答案
阅读快车系列答案
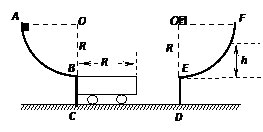 如图所示,光滑的
如图所示,光滑的


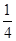 圆弧AB,半径
圆弧AB,半径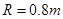 ,固定在竖直平面内。一辆质量为M=2kg的小车处在水平光滑平面上,小车的表面CD与圆弧在B点的切线重合,初始时B与C紧挨着,小车长L=1m,高H=0.2m。现有一个质量为m=1kg的滑块(可视为质点),自圆弧上的A点从静止开始释放,滑块运动到B点后冲上小车,带动小车向右运动,当滑块与小车分离时,小车运动了
,固定在竖直平面内。一辆质量为M=2kg的小车处在水平光滑平面上,小车的表面CD与圆弧在B点的切线重合,初始时B与C紧挨着,小车长L=1m,高H=0.2m。现有一个质量为m=1kg的滑块(可视为质点),自圆弧上的A点从静止开始释放,滑块运动到B点后冲上小车,带动小车向右运动,当滑块与小车分离时,小车运动了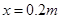 ,此时小车的速度为
,此时小车的速度为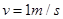 。求
。求