题目内容
(9分) 如图所示,光滑的 圆弧AB(质量可忽略)固定在甲车的左端,其半径R=1m。质量均为M=3 kg的甲、乙两辆小车静止于光滑水平面上,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离)。其中甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.4。将质量为m=2 kg的滑块P(可视为质点)从A处由静止释放,滑块P滑上乙车后最终未滑离乙车。求:
圆弧AB(质量可忽略)固定在甲车的左端,其半径R=1m。质量均为M=3 kg的甲、乙两辆小车静止于光滑水平面上,两车之间通过一感应开关相连(当滑块滑过感应开关时,两车自动分离)。其中甲车上表面光滑,乙车上表面与滑块P之间的动摩擦因数μ=0.4。将质量为m=2 kg的滑块P(可视为质点)从A处由静止释放,滑块P滑上乙车后最终未滑离乙车。求:

(i)滑块P刚滑上乙车时的速度大小;
(ii)滑块P在乙车上滑行的距离为多大?
【答案】
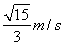

【解析】
试题分析:(i)设滑块P刚滑上乙车时的速度为v1,此时两车的速度为v2,对整体应用动量守恒和能量关系有:
mv1-2Mv2=0 (1分)
mgR=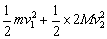 (2分)
(2分)
解得:v1=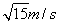
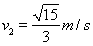 (1分)
(1分)
(ii)设滑块P和小车乙达到的共同速度为v,滑块P在乙车上滑行的距离为L,对滑块P和小车乙应用动量守恒和能量关系有:
mv1-Mv2=(m+M)v (2分)
μmgL=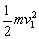 +
+ -
-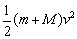 (2分)
(2分)
解得: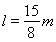 (1分)
(1分)
考点:本题考查动量守恒定律。

练习册系列答案
相关题目





