题目内容
(2008?丰台区一模)如图所示,光滑的圆弧轨道AB、EF,半径AO、O′F均为R且水平.质量为m、长度也为R的小车静止在光滑水平面CD上,小车上表面与轨道AB、EF的末端B、E相切.一质量为m的物体(可视为质点)从轨道AB的A点由静止下滑,由末端B滑上小车,小车立即向右运动.当小车右端与壁DE刚接触时,物体m恰好滑动到小车右端且相对于小车静止,同时小车与壁DE相碰后立即停止运动但不粘连,物体继续运动滑上圆弧轨道EF,以后又滑下来冲上小车.求:

(1)水平面CD的长度和物体m滑上轨道EF的最高点相对于E点的高度h;
(2)当物体再从轨道EF滑下并滑上小车后,小车立即向左运动.如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端多远?

(1)水平面CD的长度和物体m滑上轨道EF的最高点相对于E点的高度h;
(2)当物体再从轨道EF滑下并滑上小车后,小车立即向左运动.如果小车与壁BC相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端多远?
分析:(1)设物体从A滑至B点时速度为v0,在m与小车相互作用过程中,系统动量守恒,分别以物体和小车作为研究对象,根据机械能守恒联立方程即可求解;
(2)物体从CD滑下后与小车达到相对静止,有共同速度,结合动能定理对小车和物体分析,分别求出物体相对小车的位移和小车滑行的位移.从而得出Q点距小车右端的距离.
(2)物体从CD滑下后与小车达到相对静止,有共同速度,结合动能定理对小车和物体分析,分别求出物体相对小车的位移和小车滑行的位移.从而得出Q点距小车右端的距离.
解答:解:
(1)设物体从A滑至B点时速度为v0,根据机械能守恒有:mgR=
由已知,m与小车相互作用过程中,系统动量守恒
mv0=2mv1
设二者之间摩擦力为f,
以物体为研究对象:-f?sCD=
m
-
m
以车为研究对象:f(sCD-R)=
m
解得:sCD=
R
车与ED相碰后,m以速度v1冲上EF
=mgh
解得:h=
(2)由第(1)问可求得 f=
mgv1=
由能量守恒:mgR>fR+fx
mgR>
mgR+
mgx
解得 x<R 所以物体不能再滑上AB
即在车与BC相碰之前,车与物体会达到相对静止,设它们再次达到共同速度为v2:
则有:mv1=2mv2
相对静止前,物体相对车滑行距离s1
fs1=
m
-
×2m
s1=
R
车停止后,物体将做匀减速运动,相对车滑行距离s2
a=
2as2=v22
s2=
R
物体最后距车右端:
s总=s1+s2=
R
答:(1)水平面CD的长度和物体m滑上轨道EF的最高点相对于E点的高度h为
;
(2)Q点距小车右端的距离为
R
(1)设物体从A滑至B点时速度为v0,根据机械能守恒有:mgR=
| 1 |
| 2 |
| mv | 2 0 |
由已知,m与小车相互作用过程中,系统动量守恒
mv0=2mv1
设二者之间摩擦力为f,
以物体为研究对象:-f?sCD=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
以车为研究对象:f(sCD-R)=
| 1 |
| 2 |
| v | 2 1 |
解得:sCD=
| 3 |
| 2 |
车与ED相碰后,m以速度v1冲上EF
| 1 |
| 2 |
| mv | 2 1 |
解得:h=
| R |
| 4 |
(2)由第(1)问可求得 f=
| 1 |
| 2 |
|
由能量守恒:mgR>fR+fx
mgR>
| 1 |
| 2 |
| 1 |
| 2 |
解得 x<R 所以物体不能再滑上AB
即在车与BC相碰之前,车与物体会达到相对静止,设它们再次达到共同速度为v2:
则有:mv1=2mv2
相对静止前,物体相对车滑行距离s1
fs1=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
s1=
| 1 |
| 4 |
车停止后,物体将做匀减速运动,相对车滑行距离s2
a=
| f |
| m |
2as2=v22
s2=
| 1 |
| 8 |
物体最后距车右端:
s总=s1+s2=
| 3 |
| 8 |
答:(1)水平面CD的长度和物体m滑上轨道EF的最高点相对于E点的高度h为
| R |
| 4 |
(2)Q点距小车右端的距离为
| 3 |
| 8 |
点评:本题综合考查了动能定理、机械能守恒定律以及能量守恒定律,关键是理清运动的规程,选择合适的规律进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2008?丰台区一模)如图所示,在磁感应强度为B的匀强磁场中,有一匝数为N的矩形线圈,其面积为S,电阻为r,线圈两端外接一电阻为R的用电器和一个交流电压表.若线圈绕对称轴OO′以角速度ω做匀速转动,则线圈从图示位置转过90°的过程中,下列说法正确的是( )
(2008?丰台区一模)如图所示,在磁感应强度为B的匀强磁场中,有一匝数为N的矩形线圈,其面积为S,电阻为r,线圈两端外接一电阻为R的用电器和一个交流电压表.若线圈绕对称轴OO′以角速度ω做匀速转动,则线圈从图示位置转过90°的过程中,下列说法正确的是( )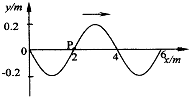 (2008?丰台区三模)如图所示是一列简谐横波在t=0时刻的波形图,已知这列波沿x轴正方向传播,波速为20m/s,则在t=0.17s时刻,质点P( )
(2008?丰台区三模)如图所示是一列简谐横波在t=0时刻的波形图,已知这列波沿x轴正方向传播,波速为20m/s,则在t=0.17s时刻,质点P( )