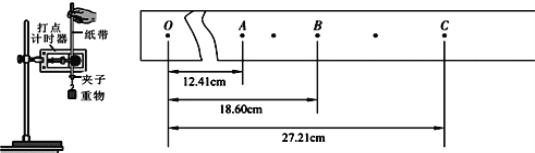
题目内容
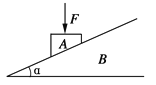
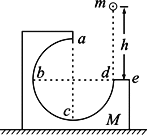
【题目】如图所示，M为固定在水平桌面上的有缺口的方形木块，abcd为
圆周的轨道，a为轨道的最高点，de面水平且有一定长度。今将质量为m的小球在d点的正上方高为h处由静止释放，让其自由下落到d处切入轨道内运动，不计空气阻力，重力加速度为
。则
A. 若轨道光滑，只要改变h的大小，就能使小球通过a点后，既可能落回轨道内，又可能落到de面上
B. 若轨道光滑，无论怎样改变h的大小，都不可能使小球通过a点后落回轨道内
C. 若轨道粗糙，小球从
处由静止释放，通过a点落到de面上且水平飞行距离为
，则小球在轨道上克服摩擦做功为
D. 若轨道粗糙，小球从处由静止释放，通过a点落到de面上且水平飞行距离为，则小球在轨道上克服摩擦做功为
【答案】BD
【解析】
A、B、若轨道光滑，从释放点到a点只有重力做功机械能守恒，
，而顺利通过a点需要满足
，从a点平抛有
，
，可得
、
，故能过a需满足，而过a点后一定落到de面；故A错误，B正确.
C、D、轨道粗糙时，通过a点落到de面上的平抛
，，可得
；从2h处释放到a点由动能定理有
，解得
；故C错误，D正确.
故选BD.
练习册系列答案
相关题目
