题目内容
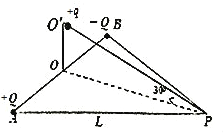
【题目】如图所示,水平面内的等边三角形 ABP 的边长为 L,顶点 P 恰好位于一倾角为 30°的光滑绝缘直轨道 O'P 的最低点,O'O 垂直于水平面,O 为三角形 AB 边的中点,现将一对等量异种电荷固定 于 A、B 两点,各自所带电荷量为 Q,在光滑直导轨 O'P 上端 O'处将质量为 m,带电荷量为+q 的小 球套在轨道上(忽略它对原电场的影响)由静止开始释放,取无穷远处电势为零,静电力常量为 k, 重力加速度为 g,空气阻力可忽略,则小球沿轨道 O'P 下滑过程中( )
A. 小球做匀加速直线运动
B. 小球的电势能先增大后减小
C. 轨道 O'与 P 处场强大小之比为 2![]() : 1
: 1
D. 小球到达轨道底端 P 的速度为![]()
【答案】ACD
【解析】
在O′点电场强度方向水平向右,则加速度由重力沿斜面向下的分量产生:a=gsin30°=0.5g,所以小球做匀加速直线运动,故A正确;因等量异种电荷固定于A、B两点,则在其连线的中垂面上所有点的场强方向垂直于该面,则为等势面,则小球O'P下滑过程中电势能不变,故B错误;对于O′点,![]() ,
, ![]() ,则
,则![]() ,∠O′AO=45°,则其场强为
,∠O′AO=45°,则其场强为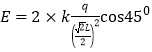 ,对于P点:
,对于P点:![]() ,则
,则![]() ,故C正确;因由O′点到P点电势相等,电场力不做功,只有重力做功:
,故C正确;因由O′点到P点电势相等,电场力不做功,只有重力做功:![]() ,解得:
,解得:![]() ,故D正确。所以ACD正确,B错误。
,故D正确。所以ACD正确,B错误。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目