题目内容
6.物体做平抛运动,抛出时间为t1时水平位移大小为竖直位移大小的2倍,抛出时间为t2时水平位移和竖直位移大小相等.则t1、t2时间内物体的水平位移x、竖直位移y、合位移s和瞬时速度v的关系,下面比例关系正确的是( )| A. | x1:x2=1:2 | B. | y1:y2=1:3 | C. | v1:v2=$\sqrt{2}$:$\sqrt{5}$ | D. | s1:s2=$\sqrt{5}$:$\sqrt{2}$ |
分析 根据水平位移和竖直位移的关系求出运动的时间,根据运动学公式求出水平位移和竖直位移以及竖直分速度,从而得出瞬时速度的大小.
解答 解:抛出时间为t1时水平位移大小为竖直位移大小的2倍,有:${v}_{0}{t}_{1}=2×\frac{1}{2}g{{t}_{1}}^{2}$,解得${t}_{1}=\frac{{v}_{0}}{g}$,则水平位移${x}_{1}={v}_{0}{t}_{1}=\frac{{{v}_{0}}^{2}}{g}$,竖直位移${y}_{1}=\frac{{{v}_{0}}^{2}}{2g}$,此时竖直分速度vy=gt=v0,根据平行四边形定则知,瞬时速度${v}_{1}=\sqrt{2}{v}_{0}$.合位移${s}_{1}=\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}=\frac{\sqrt{5}{{v}_{0}}^{2}}{2g}$,
抛出时间为t2时水平位移和竖直位移大小相等,有:${v}_{0}{t}_{2}=\frac{1}{2}g{{t}_{2}}^{2}$,解得${t}_{2}=\frac{2{v}_{0}}{g}$,则水平位移${x}_{2}={v}_{0}{t}_{2}=\frac{2{{v}_{0}}^{2}}{g}$,竖直位移${y}_{2}=\frac{2{{v}_{0}}^{2}}{g}$,此时竖直分速度vy′=gt2=2v0,根据平行四边形定则知,瞬时速度${v}_{2}=\sqrt{5}{v}_{0}$,合位移${s}_{2}=\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$
所以x1:x2=1:2,y1:y2=1:4,${v}_{1}:{v}_{2}=\sqrt{2}:\sqrt{5}$,${s}_{1}:{s}_{2}=\sqrt{5}:4\sqrt{2}$,故A、C正确,B、D错误.
故选:AC.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,难度不大.

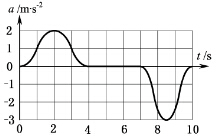 一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )
一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则人对地板的压力( )| A. | t=2s时最大 | B. | t=2s时最小 | C. | t=8.5s时最大 | D. | t=8.5s时最小 |
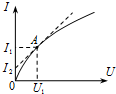 如图所示为一小灯泡的伏安特性曲线,横轴和纵轴分别表示电压U和电流I.图线上点A的坐标为(U1,I1),过点A的切线与纵轴交点的纵坐标为(0,I2).当小灯泡两端电压为U1时,其电阻等于( )
如图所示为一小灯泡的伏安特性曲线,横轴和纵轴分别表示电压U和电流I.图线上点A的坐标为(U1,I1),过点A的切线与纵轴交点的纵坐标为(0,I2).当小灯泡两端电压为U1时,其电阻等于( )| A. | $\frac{{I}_{1}}{{U}_{1}}$ | B. | $\frac{{U}_{1}}{{I}_{1}}$ | C. | $\frac{{U}_{1}}{{I}_{2}}$ | D. | $\frac{{U}_{1}}{{I}_{1}-{I}_{2}}$ |
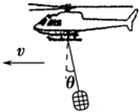 2015年4月25日14时11分,尼泊尔(北纬28.2度,东经84.7度)发生8.1级地震,一运送救灾物资的直升飞机沿水平方向匀速飞行.已知物资的总质量为m,吊运物资的悬索与竖直方向成θ角.设物资所受的空气阻力为f,悬索对物资的拉力为T,重力加速度为g,则( )
2015年4月25日14时11分,尼泊尔(北纬28.2度,东经84.7度)发生8.1级地震,一运送救灾物资的直升飞机沿水平方向匀速飞行.已知物资的总质量为m,吊运物资的悬索与竖直方向成θ角.设物资所受的空气阻力为f,悬索对物资的拉力为T,重力加速度为g,则( )| A. | f=mgsinθ | B. | f=mgtanθ | C. | T=mgcosθ | D. | T=$\frac{mg}{tanθ}$ |
| A. | 热量能够自发地从高温物体传递到低温物体,也能自发地从低温物体传递到高温物体 | |
| B. | 把很多小的单晶体放在一起,就变成了非晶体 | |
| C. | 布朗运动是液体分子对悬浮固体颗粒的碰撞作用的不平衡造成的 | |
| D. | 第二类永动机虽然不违反能量守恒定律,但它是制造不出来的. | |
| E. | 气体压强本质上就是大量气体分子作用在器壁单位面积上的平均作用力 |
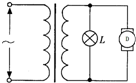 如图所示为降温所用的一个小型电风扇电路简图,其中理想变压器的原、副线圈的匝数比为22:1,原线圈接电压为U=220v的交流电源,输出端接有一只电阻为R=10Ω的灯泡和风扇电动机D,电动机线圈电阻为r=2Ω.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I=1A,则下列说法正确的是( )
如图所示为降温所用的一个小型电风扇电路简图,其中理想变压器的原、副线圈的匝数比为22:1,原线圈接电压为U=220v的交流电源,输出端接有一只电阻为R=10Ω的灯泡和风扇电动机D,电动机线圈电阻为r=2Ω.接通电源后,电风扇正常运转,测出通过风扇电动机的电流为I=1A,则下列说法正确的是( )| A. | 风扇电动机D两端的电压为2v | |
| B. | 理想变压器的输入功率为10w | |
| C. | 风扇电动机D输出的机械功率为8w | |
| D. | 若电风扇由于机械故障被卡住,则通过原线圈的电流为$\frac{3}{11}$A |

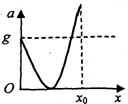
 如图所示,一根轻质弹簧竖直放置在水平面上且下端固定.一质量为m的物体从上方自由下落到弹簧上端,当弹簧的压缩量为x0时恰好减速到零,则从物体接触弹簧开始加速度大小和弹簧压缩量的关系以及速度大小和时间的关系图中可能正确的是( )
如图所示,一根轻质弹簧竖直放置在水平面上且下端固定.一质量为m的物体从上方自由下落到弹簧上端,当弹簧的压缩量为x0时恰好减速到零,则从物体接触弹簧开始加速度大小和弹簧压缩量的关系以及速度大小和时间的关系图中可能正确的是( )