题目内容
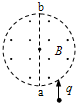如图，半径为R的圆柱形匀强磁场区域的横截面（纸面），磁感应强度大小为B，方向垂直于纸面向外．一电荷量为q（q＞0）、质量为m的粒子沿平行于直径ab的方向射入磁场区域，射入点与ab的距离为R/2．已知粒子射出磁场与射入磁场时运动方向间的夹角为60°，则粒子的速率为（不计重力）（ ）分析：由题意利用几何关系可得出粒子的转动半径，由洛仑兹力充当向心力可得出粒子速度的大小；
解答：解：粒子的偏转角是60°，即它的轨迹圆弧对应的圆心角是60，所以入射点、出射点和圆心构成等边三角形，所以，它的轨迹的半径与圆形磁场的半径相等，即r=R．
洛伦兹力提供向心力：qvB=
，变形得：v=
．故正确的答案是B．
故选：B
洛伦兹力提供向心力：qvB=
| mv2 |
| R |
| qBR |
| m |
故选：B
点评：在磁场中做圆周运动，确定圆心和半径为解题的关键．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
风洞实验室可产生水平方向的、大小可调节的风力．在风洞中有一个固定的支撑架ABC，该支撑架的外表面光滑，且有一半径为R的四分之一圆柱面，支撑架固定在离地面高为2R的平台上，平台竖直侧壁光滑，如图所示，地面上的D点处有一竖直的小洞，小洞离侧壁的水平距离为R，现将质量分别为m1和m2的两个小球用一根不可伸长的轻绳连接按图示的方式置于圆柱面上，球m1放在柱面底部的A点，球m2竖直下垂．
。
。
。求两条光线经柱面和底面折射后的交点与O点的距离d。
。求两条光线经柱面和底面折射后的交点与O点的距离d。