题目内容
4. 如图所示,A、B、C三个木块的质量均为m,置于光滑的水平桌面上的同一条直线上,A、B木块之间有一轻质弹簧,弹簧的两端与木块接触而不拴接,将弹簧压缩到不能再压缩时(弹簧处在弹性限度内),用细线把A木块和B木块紧连,使弹簧不能伸展,以至于A、B木块一起可视为一个整体,现让A、B木块一起以一向右的初速度v0沿A、B的连线向静止的C而使A木块与B、C木块分离,已知A木块离开弹簧后的速度大小为$\frac{{v}_{0}}{3}$,方向水平向左,求:
如图所示,A、B、C三个木块的质量均为m,置于光滑的水平桌面上的同一条直线上,A、B木块之间有一轻质弹簧,弹簧的两端与木块接触而不拴接,将弹簧压缩到不能再压缩时(弹簧处在弹性限度内),用细线把A木块和B木块紧连,使弹簧不能伸展,以至于A、B木块一起可视为一个整体,现让A、B木块一起以一向右的初速度v0沿A、B的连线向静止的C而使A木块与B、C木块分离,已知A木块离开弹簧后的速度大小为$\frac{{v}_{0}}{3}$,方向水平向左,求:(1)弹簧释放的弹性势能;
(2)从A、B木块与C木块开始碰撞到弹簧的弹性势能全部释放的过程中,木块A受到的合外力的冲量大小.
分析 (1)A、B与C碰撞过程中动量守恒,由动量守恒定律可以求出碰后三者的共同速度;线断开,BC与A分离过程中动量守恒,由动量守恒定律可以列方程;在弹簧弹开过程中,系统机械能守恒,由机械能守恒定律可以列方程,解方程即可求出弹簧的弹性势能.
(2)应用动量定理可以求出A所受合外力的冲量.
解答 解:(1)以向右为正方向,设碰后A、B和C的共同速度的大小为v1,由动量守恒定律得:
2mv0=3mv1,
解得:v1=$\frac{2}{3}$v0,
设C离开弹簧时,BC的速度大小为v1,由动量守恒得:
3mv1=2mv2-m×$\frac{1}{3}$v0,
设弹簧的弹性势能为EP,从细线断开到A与弹簧分开的过程中机械能守恒,有:
$\frac{1}{2}$(3m)v12+EP=$\frac{1}{2}$(2m)v22+$\frac{1}{2}$m($\frac{1}{3}$v0)2,
解得:EP=$\frac{3}{4}$mv02 ;
(2)在整个过程中,对A由动量定理得:I=-m$\frac{{v}_{0}}{3}$-mv0=-$\frac{4}{3}$mv0,负号表示方向向左;
答:(1)弹簧释放的弹性势能为$\frac{3}{4}$mv02 ;
(2)从A、B木块与C木块开始碰撞到弹簧的弹性势能全部释放的过程中,木块A受到的合外力的冲量大小为$\frac{4}{3}$mv0.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程是 解题的关键,应用动量守恒定律、机械能守恒定律与动量定理可以解题;解题时要注意正方向的选择.

练习册系列答案
相关题目
14. 如图所示,小球A位于斜面上,小球B与小球A位于同一高度,现将小球A,B分别以v1和v2的速度水平抛出,都落在了倾角为45°的斜面上的同一点,且小球恰好垂直打到斜面上,则v1:v2为( )
如图所示,小球A位于斜面上,小球B与小球A位于同一高度,现将小球A,B分别以v1和v2的速度水平抛出,都落在了倾角为45°的斜面上的同一点,且小球恰好垂直打到斜面上,则v1:v2为( )
 如图所示,小球A位于斜面上,小球B与小球A位于同一高度,现将小球A,B分别以v1和v2的速度水平抛出,都落在了倾角为45°的斜面上的同一点,且小球恰好垂直打到斜面上,则v1:v2为( )
如图所示,小球A位于斜面上,小球B与小球A位于同一高度,现将小球A,B分别以v1和v2的速度水平抛出,都落在了倾角为45°的斜面上的同一点,且小球恰好垂直打到斜面上,则v1:v2为( )| A. | 3:2 | B. | 2:1 | C. | 1:1 | D. | 1:2 |
15.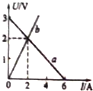 如图所示,直线a为某电源的路端电压随电流变化的图线,直线b为电阻R两端的电压与电流关系的图线,用该电源和该电阻组成的闭合电路,电源的输出功率和电源的内电阻分别为( )
如图所示,直线a为某电源的路端电压随电流变化的图线,直线b为电阻R两端的电压与电流关系的图线,用该电源和该电阻组成的闭合电路,电源的输出功率和电源的内电阻分别为( )
 如图所示,直线a为某电源的路端电压随电流变化的图线,直线b为电阻R两端的电压与电流关系的图线,用该电源和该电阻组成的闭合电路,电源的输出功率和电源的内电阻分别为( )
如图所示,直线a为某电源的路端电压随电流变化的图线,直线b为电阻R两端的电压与电流关系的图线,用该电源和该电阻组成的闭合电路,电源的输出功率和电源的内电阻分别为( )| A. | 2W | B. | 4W | C. | 0.5Ω | D. | 1Ω |
12. 如图所示,一个内壁光滑的绝缘细直管竖直放置,在管子的底部固定一电荷量为Q(Q>0)的点电荷.在距离底部点电荷为h2的管口A处,有一电荷量为q(q>0)、质量为m的点电荷由静止释放,在距离底部点电荷为h1的B处速度恰好为零.现让一个电荷量为q、质量为3m的点电荷仍在A处由静止释放,已知静电力常量为k,重力加速度为g,则该点电荷( )
如图所示,一个内壁光滑的绝缘细直管竖直放置,在管子的底部固定一电荷量为Q(Q>0)的点电荷.在距离底部点电荷为h2的管口A处,有一电荷量为q(q>0)、质量为m的点电荷由静止释放,在距离底部点电荷为h1的B处速度恰好为零.现让一个电荷量为q、质量为3m的点电荷仍在A处由静止释放,已知静电力常量为k,重力加速度为g,则该点电荷( )
 如图所示,一个内壁光滑的绝缘细直管竖直放置,在管子的底部固定一电荷量为Q(Q>0)的点电荷.在距离底部点电荷为h2的管口A处,有一电荷量为q(q>0)、质量为m的点电荷由静止释放,在距离底部点电荷为h1的B处速度恰好为零.现让一个电荷量为q、质量为3m的点电荷仍在A处由静止释放,已知静电力常量为k,重力加速度为g,则该点电荷( )
如图所示,一个内壁光滑的绝缘细直管竖直放置,在管子的底部固定一电荷量为Q(Q>0)的点电荷.在距离底部点电荷为h2的管口A处,有一电荷量为q(q>0)、质量为m的点电荷由静止释放,在距离底部点电荷为h1的B处速度恰好为零.现让一个电荷量为q、质量为3m的点电荷仍在A处由静止释放,已知静电力常量为k,重力加速度为g,则该点电荷( )| A. | 运动到B处的速度大小为$\frac{2}{3}\sqrt{3g({h}_{2}-{h}_{1})}$ | |
| B. | 速度最大处与底部点电荷距离为$\sqrt{\frac{kQq}{mg}}$ | |
| C. | 在下落过程中电势能逐渐减小 | |
| D. | 在下落过程中加速度逐渐减小 |
19.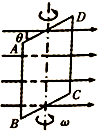 如图,矩形线圈ABCD放在匀强磁场中,绕一在线圈平面内垂直于磁感线的轴匀速转动,其角速度大小为ω=2πrad/s,线圈的匝数N=50匝,线圈围成的面积为1m2,线圈的电阻为R=10,匀强磁场的磁感应强度大小为B=0.2T,若从图示时刻(线圈平面与磁场方向的夹角θ=45°)开始计时,并且设电流流向ABCD为正,则( )
如图,矩形线圈ABCD放在匀强磁场中,绕一在线圈平面内垂直于磁感线的轴匀速转动,其角速度大小为ω=2πrad/s,线圈的匝数N=50匝,线圈围成的面积为1m2,线圈的电阻为R=10,匀强磁场的磁感应强度大小为B=0.2T,若从图示时刻(线圈平面与磁场方向的夹角θ=45°)开始计时,并且设电流流向ABCD为正,则( )
 如图,矩形线圈ABCD放在匀强磁场中,绕一在线圈平面内垂直于磁感线的轴匀速转动,其角速度大小为ω=2πrad/s,线圈的匝数N=50匝,线圈围成的面积为1m2,线圈的电阻为R=10,匀强磁场的磁感应强度大小为B=0.2T,若从图示时刻(线圈平面与磁场方向的夹角θ=45°)开始计时,并且设电流流向ABCD为正,则( )
如图,矩形线圈ABCD放在匀强磁场中,绕一在线圈平面内垂直于磁感线的轴匀速转动,其角速度大小为ω=2πrad/s,线圈的匝数N=50匝,线圈围成的面积为1m2,线圈的电阻为R=10,匀强磁场的磁感应强度大小为B=0.2T,若从图示时刻(线圈平面与磁场方向的夹角θ=45°)开始计时,并且设电流流向ABCD为正,则( )| A. | 该交变电流的频率为1Hz | |
| B. | 改交变电流的表达式i=2sin(2t-$\frac{π}{4}$)A | |
| C. | 线圈中产生电功率为40W | |
| D. | 线圈中电流的方向每分钟改变120次 |
9.下列说法中正确的是( )
| A. | 物体的质量越大,受到的重力也越大,所以物体的重力是由物体的质量产生的 | |
| B. | 物体的重力就是地球对它的吸引力 | |
| C. | 木块放在桌面上对桌面的压力是由于木块发生微小形变而产生的 | |
| D. | 互相接触的两个物体间一定存在相互作用的弹力 |
16.关于电容下列说法不正确的是( )
| A. | 平行板电容器极板正对面积越大,电容器的电容就越大 | |
| B. | 平行板电容器极板间的距离越大,电容器的电容就越大 | |
| C. | 极板间的电介质的性质会影响电容器的电容 | |
| D. | 电容器既能充电也能放电 |
14.在做“验证力的平行四边形定则”实验时,橡皮条的一端固定在木板上,一次用两个弹簧秤分别拉着两根绳套把橡皮条的另一端拉到某一确定的O点,另一次是用一个弹簧秤通过细绳把橡皮条的另一端拉到O点,则下列说法中正确的是( )
| A. | 同一次实验中,O点位置不允许变动 | |
| B. | 实验中,橡皮条、细绳和弹簧秤应与木板保持平行 | |
| C. | 实验中,把橡皮条的另一端拉到O点时,两个弹簧秤之间的夹角必须取90° | |
| D. | 拉橡皮条的细绳要适当长些,标记同一细绳方向的两点要稍远些 |
