题目内容
20.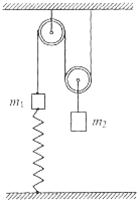 如图所示,装置中绳子质量、滑轮质量及摩擦均不计,两物体质量分别为m1=m,m2=4m,m1下端通过劲度系数为k的轻质弹簧与地面相连.
如图所示,装置中绳子质量、滑轮质量及摩擦均不计,两物体质量分别为m1=m,m2=4m,m1下端通过劲度系数为k的轻质弹簧与地面相连.(1)系统静止时弹簧处于什么状态?形变量△x为多少?
(2)用手托住m2,让m1静止在弹簧上,弹簧刚好无形变,然后放手,当m2下落h刚好至最低点时,弹簧的弹性势能多大?
分析 (1)滑轮的特性分析拉m1的绳子拉力大小,判断弹簧的状态;根据平衡条件和胡克定律求解形变量△x.
(2)m2下落h的过程中,两个物体和弹簧组成的系统机械能守恒,由机械能守恒定律和几何知识列式求解即可.
解答 解:(1)由图分析可知,拉m1的绳子拉力大小为 T=2mg,大于mg,所以弹簧处于拉伸状态.根据平衡条件得:
对m1:T=m1g+k△x=mg+k△x
对m2:2T=m2g=4mg
联立解得:△x=$\frac{mg}{k}$
②当m2下落h时,m1上升$\frac{1}{2}$h,根据两个物体和弹簧组成的系统机械能守恒得:
m2gh=m1g•$\frac{1}{2}$h+Ep;
解得 Ep=3.5mgh
答:
(1)系统静止时弹簧处于拉伸状态,伸长量△x为$\frac{mg}{k}$.
(2)当m2下落h刚好至最低点时,弹簧的弹性势能是3.5mgh.
点评 本题是连接体问题,关键要抓住滑轮的力学特性和系统的机械能守恒,要注意两个物体下落和上升的高度不等,要根据滑轮的特性研究.

练习册系列答案
相关题目
8.下列关于路程和位移的说法中,正确的是( )
| A. | 物体沿直线运动时,位移的大小一定等于路程 | |
| B. | 路程为零时,位移不一定为零 | |
| C. | 位移为零时,路程不一定为零 | |
| D. | 物体沿曲线运动时,位移的大小可以等于路程 |
15.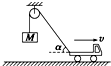 如图,汽车向右沿水平面运动,通过绳子提升重物M.若不计绳子质量和绳子与滑轮间的摩擦,则在重物匀速上升的过程中,有( )
如图,汽车向右沿水平面运动,通过绳子提升重物M.若不计绳子质量和绳子与滑轮间的摩擦,则在重物匀速上升的过程中,有( )
 如图,汽车向右沿水平面运动,通过绳子提升重物M.若不计绳子质量和绳子与滑轮间的摩擦,则在重物匀速上升的过程中,有( )
如图,汽车向右沿水平面运动,通过绳子提升重物M.若不计绳子质量和绳子与滑轮间的摩擦,则在重物匀速上升的过程中,有( )| A. | 汽车做加速运动 | B. | 汽车做减速运动 | ||
| C. | 地面对汽车的支持力增大 | D. | 绳子张力不断减小 |
5.下列所描述的运动中,不可能的有( )
| A. | 速度变化很大,加速度很小 | |
| B. | 速度变化方向为正,加速度方向为正 | |
| C. | 速度变化越来越快,加速度越来越小 | |
| D. | 速度越来越大,加速度越来越小 |
12.下列说法正确的有( )
| A. | 曲线运动的速度一定是要改变的 | |
| B. | 曲线运动一定不是匀变速运动 | |
| C. | 合运动的时间一定比分运动的时间长 | |
| D. | 只要确定了两个分速度的大小,就可以确定合速度的大小 |
9.关于电阻的计算式R=$\frac{U}{I}$和决定式R=ρ$\frac{L}{S}$,下面说法正确的是( )
| A. | 导体的电阻与电阻两端的电压成正比,与电流成反比 | |
| B. | 导体的电阻仅与导体长度、横截面积和材料有关 | |
| C. | 导体的电阻与工作温度无关 | |
| D. | 对于一定的导体来说,在恒温下比值$\frac{U}{I}$是恒定的,导体电阻不随U或I的变化而变化 |
 如图所示,物体沿x轴做直线运动,从A点运动到B点.写出A点坐标、B点坐标,并求出从A点到B点走过的位移.
如图所示,物体沿x轴做直线运动,从A点运动到B点.写出A点坐标、B点坐标,并求出从A点到B点走过的位移.