题目内容
1.地面上方较高的某一点处有A、B两个小球(可视为质点),中间用长为L的轻绳相连,当A球以v0大小的速度水平抛出的同时,B球以同样大小的初速度竖直向下抛出,若不计空气阻力,重力加速度为g.求:(1)抛出多久,绳刚好拉直?
(2)从抛出到绳拉直过程中,A球的位移多大?
分析 (1)A球做平抛运动,B球竖直下抛,当它们之间的距离等于绳长的时候绳刚好拉直,利用几何关系来来计算时间的大小;
(2)位移是矢量,根据水平和竖直方向上的位移求它们的矢量合;
解答 解:(1)A球做平抛运动x=v0t
${h_1}=\frac{1}{2}g{t^2}$
B球竖直下抛:${h_2}={v_0}t+\frac{1}{2}g{t^2}$
AB之间的距离为绳长的时候,
${L^2}={({v_0}t)^2}+{({h_2}-{h_1})^2}$
解得:$t=\frac{{\sqrt{2}L}}{{2{v_0}}}$
(2)A球做的是平抛运动,合位移的大小为:
$S=\sqrt{{x^2}+{h_1}^2}$=$\sqrt{\frac{L^2}{2}+{{(\frac{{8{L^2}}}{{4{v_0}^2}})}^2}}$=$\frac{L}{{4{v_0}^2}}\sqrt{8{v_0}^4+{g^2}{L^2}}$,
答:(1)经过时间$\frac{\sqrt{2}L}{2{v}_{0}}$,绳刚好拉直;
(2)从抛出到绳拉直过程中,A球的位移大小为$\frac{L}{{4{v_0}^2}}\sqrt{8{v_0}^4+{g^2}{L^2}}$.
点评 本题是对平抛运动和竖直下抛运动规律的考查,本题的关键是分析清楚,绳被拉直时,它们之间的距离等于绳长.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
3. 有一质量为M,半径为R,密度均匀的球体,在距离球心O为2R的地方有一质量为m的质点,现从M中挖去半径为$\frac{1}{2}$R的球体,如图所示,则剩余部分对m的万有引力F为( )
有一质量为M,半径为R,密度均匀的球体,在距离球心O为2R的地方有一质量为m的质点,现从M中挖去半径为$\frac{1}{2}$R的球体,如图所示,则剩余部分对m的万有引力F为( )
 有一质量为M,半径为R,密度均匀的球体,在距离球心O为2R的地方有一质量为m的质点,现从M中挖去半径为$\frac{1}{2}$R的球体,如图所示,则剩余部分对m的万有引力F为( )
有一质量为M,半径为R,密度均匀的球体,在距离球心O为2R的地方有一质量为m的质点,现从M中挖去半径为$\frac{1}{2}$R的球体,如图所示,则剩余部分对m的万有引力F为( )| A. | $\frac{7GMm}{{36R}^{2}}$ | B. | $\frac{7GMm}{{8R}^{2}}$ | C. | $\frac{GMm}{{18R}^{2}}$ | D. | $\frac{7GMm}{{32R}^{2}}$ |
6. 空间中有一方向沿竖直平面的匀强电场,另有一光滑绝缘杆,杆上套有电荷量为+Q质量为m的小球,现在电场所在竖直平面内将杆分别置于OA、OB、OC三个不同位置,其中OA为水平,OC竖直,OB与水平面夹角60°.小球分别从杆端A、B、C静止释放,已知小球从A到O运动时间为从B到O运动时间的$\sqrt{2}$倍,则可判断( )
空间中有一方向沿竖直平面的匀强电场,另有一光滑绝缘杆,杆上套有电荷量为+Q质量为m的小球,现在电场所在竖直平面内将杆分别置于OA、OB、OC三个不同位置,其中OA为水平,OC竖直,OB与水平面夹角60°.小球分别从杆端A、B、C静止释放,已知小球从A到O运动时间为从B到O运动时间的$\sqrt{2}$倍,则可判断( )
 空间中有一方向沿竖直平面的匀强电场,另有一光滑绝缘杆,杆上套有电荷量为+Q质量为m的小球,现在电场所在竖直平面内将杆分别置于OA、OB、OC三个不同位置,其中OA为水平,OC竖直,OB与水平面夹角60°.小球分别从杆端A、B、C静止释放,已知小球从A到O运动时间为从B到O运动时间的$\sqrt{2}$倍,则可判断( )
空间中有一方向沿竖直平面的匀强电场,另有一光滑绝缘杆,杆上套有电荷量为+Q质量为m的小球,现在电场所在竖直平面内将杆分别置于OA、OB、OC三个不同位置,其中OA为水平,OC竖直,OB与水平面夹角60°.小球分别从杆端A、B、C静止释放,已知小球从A到O运动时间为从B到O运动时间的$\sqrt{2}$倍,则可判断( )| A. | 从C到O方向运动的时间小于从A到O的时间 | |
| B. | 从C到O方向运动的时间大于从A到O的时间 | |
| C. | 电场强度的最小值为$\frac{mg}{2Q}$ | |
| D. | 电场强度的最小值为$\frac{\sqrt{3}mg}{3Q}$ |
10.2009年2月11日,美国和俄罗斯的两颗卫星在西伯利亚上空相撞,这是有史以来首次卫星碰撞事件,碰撞点比相对地球静止的国际空间站高434km.则以下说法中正确的是( )
| A. | 在碰撞点高度沿圆周运行的卫星的周期比国际空间站的周期大 | |
| B. | 在碰撞点高度沿圆周运行的卫星的加速度比空间站的加速度小 | |
| C. | 在与空间站相同轨道上运行的卫星一旦加速,稳定运行后,运行周期一定减小 | |
| D. | 空间站可能经过中国东北地区某位置的正上方 |
 如图所示,一单摆摆长为L,摆球质量为m,悬挂于O点.现将小球拉至P点,然后释放,使小球做简谐运动,小球偏离竖直方向的最大角度为θ.己知重力加速度为g.在小球由P点运动到最低点P′的过程中小球所受重力的冲量为$\frac{1}{2}$πm$\sqrt{gL}$,小球所受合力的冲量为m$\sqrt{2gL(1-cosθ)}$.
如图所示,一单摆摆长为L,摆球质量为m,悬挂于O点.现将小球拉至P点,然后释放,使小球做简谐运动,小球偏离竖直方向的最大角度为θ.己知重力加速度为g.在小球由P点运动到最低点P′的过程中小球所受重力的冲量为$\frac{1}{2}$πm$\sqrt{gL}$,小球所受合力的冲量为m$\sqrt{2gL(1-cosθ)}$. 利用如图装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的质量相等,当系统达到平衡时,根据钩码个数读出三根绳子的拉力分别为FOA,FOB,FOC,回答下列问题
利用如图装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的质量相等,当系统达到平衡时,根据钩码个数读出三根绳子的拉力分别为FOA,FOB,FOC,回答下列问题 如图甲所示,固定在水平桌边上的L双轨型平行金属导轨足够长,倾角为θ=53°,间距L=2m,电阻不计;导轨上两根金属棒ab、cd的阻值分别为R1=25Ω,R2=4Ω,ab棒的质量m1=5.0kg,cd棒质量m2=1.0kg,ab与导轨间的动摩擦因数μ1=$\frac{2}{15}$,cd与导轨间的动摩擦因数μ2=0.5,设最大静摩擦力等于滑动摩擦力,整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中.现让ab棒从导轨上离桌面某一高度处由静止释放,当它刚要滑出导轨时,cd棒也恰好开始滑动,且ab棒下滑阶段,通过ab棒的电荷量为q=2C;g取10m/s2.
如图甲所示,固定在水平桌边上的L双轨型平行金属导轨足够长,倾角为θ=53°,间距L=2m,电阻不计;导轨上两根金属棒ab、cd的阻值分别为R1=25Ω,R2=4Ω,ab棒的质量m1=5.0kg,cd棒质量m2=1.0kg,ab与导轨间的动摩擦因数μ1=$\frac{2}{15}$,cd与导轨间的动摩擦因数μ2=0.5,设最大静摩擦力等于滑动摩擦力,整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中.现让ab棒从导轨上离桌面某一高度处由静止释放,当它刚要滑出导轨时,cd棒也恰好开始滑动,且ab棒下滑阶段,通过ab棒的电荷量为q=2C;g取10m/s2.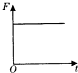 光滑水平面上静止的物体,受到一个水平拉力作用开始运动,拉力F随时间t变化的图象如图所示,用Ek、v、x、a分别表示物体的动能、速度、位移和加速度,下列四个图象分别定性描述了这些物理量随时间变化的情况,其中正确的是( )
光滑水平面上静止的物体,受到一个水平拉力作用开始运动,拉力F随时间t变化的图象如图所示,用Ek、v、x、a分别表示物体的动能、速度、位移和加速度,下列四个图象分别定性描述了这些物理量随时间变化的情况,其中正确的是( )


