题目内容
如图甲所示，水平地面上的P点有一质量m=1.0kg的滑块，一轻弹簧左端固定在墙面，右端与滑块接触（不粘连），弹簧处于原长．现推动滑块将弹簧压缩到Q点，PQ间的距离△x=0.40m．t=0时刻释放滑块，利用速度传感器描绘出滑块的速度-时间图象如图乙中的Oabc所示，其中Oab段为曲线，bc段为直线．Od是速度图象上O点的切线．取g=10m/s2．求：
（1）滑块与地面间的动摩擦因数μ；
（2）弹簧的劲度系数k．
（1）滑块与地面间的动摩擦因数μ；
（2）弹簧的劲度系数k．
分析：（1）根据速度时间图线求出匀减速直线运动的加速度，通过牛顿第二定律求出滑块与地面之间的动摩擦因数．
（2）根据速度图象的斜率等于加速度，求出刚释放弹簧瞬时滑块的加速度，根据牛顿第二定律和胡克定律列式，即可求得k．
（2）根据速度图象的斜率等于加速度，求出刚释放弹簧瞬时滑块的加速度，根据牛顿第二定律和胡克定律列式，即可求得k．
解答：解：（1）从图象上知bc段对应滑块脱离弹簧后的运动，滑块的加速度大小为：
a1=
=
=5m/s2；
由牛顿第二定律知：μmg=ma1，解得：μ=0.5
（2）由速度图象的斜率等于加速度，则知t=0时刻滑块的加速度a2=
=
=30m/s2；
根据牛顿第二定律得：k△x-μmg=ma2，解得：k=87.5N/m
答：
（1）滑块与地面间的动摩擦因数μ是0.5；
（2）弹簧的劲度系数k是87.5N/m．
a1=
| △v |
| △t |
| 1.5 |
| 0.55-0.25 |
由牛顿第二定律知：μmg=ma1，解得：μ=0.5
（2）由速度图象的斜率等于加速度，则知t=0时刻滑块的加速度a2=
| △v |
| △t |
| 3 |
| 0.1 |
根据牛顿第二定律得：k△x-μmg=ma2，解得：k=87.5N/m
答：
（1）滑块与地面间的动摩擦因数μ是0.5；
（2）弹簧的劲度系数k是87.5N/m．
点评：本题关键要由速度图象的斜率等于加速度，再根据牛顿第二定律、胡克定律结合进行求解，基础题．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图甲所示，水平平台的右端安装有轻质滑轮，质量为M=2.5kg的物块A放在与滑轮相距l的平台上，现有一轻绳跨过定滑轮，左端与物块连接，右端挂质量为m=0.5kg的小球B，绳拉直时用手托住小球使其在距地面h高处静止，绳与滑轮间的摩擦不计，重力加速度为g（g取10 m/s2）．设最大静摩擦力等于滑动摩擦力．
如图甲所示，水平天花板下悬挂一光滑的轻质的定滑轮，跨过定滑轮的质量不计的绳（绳承受拉力足够大）两端分别连接物块A和B，A的质量为m0，B的质量m是可以变化的，当B的质量改变时，可以得到A加速度变化图线如图乙所示，不计空气阻力和所有的摩擦，A加速度向上为正．
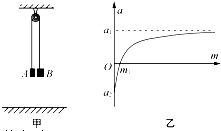如图甲所示，水平天花板下悬挂一光滑的轻质的定滑轮，跨过定滑轮的质量不计的绳（绳承受拉力足够大）两端分别连接物块A和B，A的质量为m0，B的质量m是可以变化的，当B的质量改变时，可以得到A加速度变化图线如图乙所示，不计空气阻力和所有的摩擦，A加速度向上为正．