题目内容
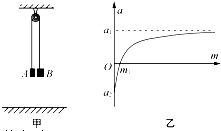 如图甲所示,水平天花板下悬挂一光滑的轻质的定滑轮,跨过定滑轮的质量不计的绳(绳承受拉力足够大)两端分别连接物块A和B,A的质量为m0,B的质量m是可以变化的,当B的质量改变时,可以得到A加速度变化图线如图乙所示,不计空气阻力和所有的摩擦,A加速度向上为正.
如图甲所示,水平天花板下悬挂一光滑的轻质的定滑轮,跨过定滑轮的质量不计的绳(绳承受拉力足够大)两端分别连接物块A和B,A的质量为m0,B的质量m是可以变化的,当B的质量改变时,可以得到A加速度变化图线如图乙所示,不计空气阻力和所有的摩擦,A加速度向上为正.(1)求图乙中a1、a2和m1的大小.
(2)根据牛顿定律和运动学规律,证明在A和B未着地或与滑轮接触时,AB系统机械能守恒.
(3)若m0=0.8kg,m=1.2kg,AB开始都在离水平地面H=0.5m处,由静止释放AB,且B着地后不反弹,求A上升离水平地面的最大高度.(g取10m/s2)
分析:(1)根据牛顿第二定律,采用隔离法分别研究A和B,得到加速度与两物体质量的关系式,由图象上读出m→∞和两坐标轴的截距,求出a1、a2和m1的大小.
(2)根据运动学公式得出速度与高度的关系,通过变形证明系统的机械能守恒.
(3)将m0=0.8kg,m=1.2kg代入加速度的表达式,求出加速度,由运动学公式求出B着地时A的速度.B着地后A做竖直上抛运动,再由运动学公式求出A上升的最大高度.
(2)根据运动学公式得出速度与高度的关系,通过变形证明系统的机械能守恒.
(3)将m0=0.8kg,m=1.2kg代入加速度的表达式,求出加速度,由运动学公式求出B着地时A的速度.B着地后A做竖直上抛运动,再由运动学公式求出A上升的最大高度.
解答:解;(1)根据牛顿第二定律得
对B:mg-F=ma
对A:F-m0g=m0a
得a=
g
当m→∞时 a1=g;
当m=0时 a2=-g;
当a=0时 m=m1=m0
(2)设A开始离水平面h1,B开始离水平面h2,由静止释放A上升到高度h1′,B下降到高度h2′,则
h1′-h1=h2-h2′=h
设AB发生h位移时速度为v,则有
v2=2ah
将a=
g代入得
v2=2
gh
变形得
(m+m0)v2=mg(h2-h2′)-m0g(h1′-h1)
得
m0v2+m0gh1′+
mv2+mgh2′=m0gh1+mgh2
故A、B系统的机械能守恒.
(3)从H=0.5m高处释放,AB加速度
a=
g=2m/s2
B着地时A的速度为 v=
=
m/s
接着A做竖直上抛运动,上升的高度为h=
=0.1m
所以A距离水平面最大高度hm=2H+h=1.1m
答:
(1)图乙中a1=g,a2=-g,m1=m0.
(2)AB系统的机械能守恒证明见上.
(3)A上升离水平地面的最大高度是1.1m.
对B:mg-F=ma
对A:F-m0g=m0a
得a=
| m-m0 |
| m+m0 |
当m→∞时 a1=g;
当m=0时 a2=-g;
当a=0时 m=m1=m0
(2)设A开始离水平面h1,B开始离水平面h2,由静止释放A上升到高度h1′,B下降到高度h2′,则
h1′-h1=h2-h2′=h
设AB发生h位移时速度为v,则有
v2=2ah
将a=
| m-m0 |
| m+m0 |
v2=2
| m-m0 |
| m+m0 |
变形得
| 1 |
| 2 |
得
| 1 |
| 2 |
| 1 |
| 2 |
故A、B系统的机械能守恒.
(3)从H=0.5m高处释放,AB加速度
a=
| m-m0 |
| m+m0 |
B着地时A的速度为 v=
| 2aH |
| 2 |
接着A做竖直上抛运动,上升的高度为h=
| v2 |
| 2g |
所以A距离水平面最大高度hm=2H+h=1.1m
答:
(1)图乙中a1=g,a2=-g,m1=m0.
(2)AB系统的机械能守恒证明见上.
(3)A上升离水平地面的最大高度是1.1m.
点评:本题考查了运用数学方法解决物理问题的能力.证明题要规范,步骤要完整,要有必要的假设.

练习册系列答案
相关题目
 如图甲所示,水平天花板下悬挂一光滑的轻质的定滑轮,跨过定滑轮的质量不计的绳(绳承受拉力足够大)两端分别连接物块A和B,A的质量为m0,B的质量m是可以变化的,当B的质量改变时,可以得到A加速度变化图线如图乙所示,不计空气阻力和所有的摩擦,A加速度向上为正.
如图甲所示,水平天花板下悬挂一光滑的轻质的定滑轮,跨过定滑轮的质量不计的绳(绳承受拉力足够大)两端分别连接物块A和B,A的质量为m0,B的质量m是可以变化的,当B的质量改变时,可以得到A加速度变化图线如图乙所示,不计空气阻力和所有的摩擦,A加速度向上为正.
 如图甲所示,水平天花板下悬挂一光滑的轻质的定滑轮,跨过定滑轮的质量不计的绳(绳承受拉力足够大)两端分别连接物块A和B,A的质量为m0,B的质量m是可以变化的,当B的质量改变时,可以得到A加速度变化图线如图乙所示,不计空气阻力和所有的摩擦,A加速度向上为正.
如图甲所示,水平天花板下悬挂一光滑的轻质的定滑轮,跨过定滑轮的质量不计的绳(绳承受拉力足够大)两端分别连接物块A和B,A的质量为m0,B的质量m是可以变化的,当B的质量改变时,可以得到A加速度变化图线如图乙所示,不计空气阻力和所有的摩擦,A加速度向上为正.