题目内容
如图甲所示，水平平台的右端安装有轻质滑轮，质量为M=2.5kg的物块A放在与滑轮相距l的平台上，现有一轻绳跨过定滑轮，左端与物块连接，右端挂质量为m=0.5kg的小球B，绳拉直时用手托住小球使其在距地面h高处静止，绳与滑轮间的摩擦不计，重力加速度为g（g取10 m/s2）．设最大静摩擦力等于滑动摩擦力．（1）某探究小组欲用上述装置测量物块与平台间的动摩擦因数．放开小球，系统运动，该小组对小球匀加速下落过程拍得同一底片上多次曝光的照片如图（乙）所示，拍摄时每隔1s曝光一次，若小球直径为20cm，求物块A与平台间的动摩擦因数μ；
（2）设小球着地后立即停止运动，已知l=3.0m，要使物块A不撞到定滑轮，求小球下落的最大高度h？（假设小球距地面足够高，计算结果保留三位有效数字）
分析：（1）根据连续相等时间内的位移之差是一恒量求出加速度的大小，分别隔离对小球和物块A分析，运用牛顿第二定律求出物块A与平台间的动摩擦因数．
（2）小球落地后，物块A做匀减速直线运动，结合牛顿第二定律和速度位移公式求出小球下落的最大高度．
（2）小球落地后，物块A做匀减速直线运动，结合牛顿第二定律和速度位移公式求出小球下落的最大高度．
解答：解（1）对照片分析知，x1=60cm，x2=100cm，
由△x=x2-x1=aT2
得 a=0.4m/s2
小球B，由 mg-FT=ma
物块A得：FT′-Ff=Ma
Ff=μMg FT=FT′
解得：μ=
=0.152．
（2）对小球A：小球做初速度为零，加速度为a的匀加速直线运动，落地时速度为v，由运动学公式有：v2-0=2ah
对物块A：B从开始下落到着地，A也运动了h，随后在摩擦力作用下做匀减速直线运动，由牛顿第二定律，有：μMg=Ma
要使物块不撞到定滑轮，则应满足v2＜2a′（l-h）
可得h＜
代入数值，解得h＜2.375m．
答：（1）物块A与平台间的动摩擦因数为0.152．
（2）小球下落的最大高度h为2.375m．
由△x=x2-x1=aT2
得 a=0.4m/s2
小球B，由 mg-FT=ma
物块A得：FT′-Ff=Ma
Ff=μMg FT=FT′
解得：μ=
| mg-(M+m)a |
| Mg |
（2）对小球A：小球做初速度为零，加速度为a的匀加速直线运动，落地时速度为v，由运动学公式有：v2-0=2ah
对物块A：B从开始下落到着地，A也运动了h，随后在摩擦力作用下做匀减速直线运动，由牛顿第二定律，有：μMg=Ma
要使物块不撞到定滑轮，则应满足v2＜2a′（l-h）
可得h＜
| a′l |
| a+a′ |
代入数值，解得h＜2.375m．
答：（1）物块A与平台间的动摩擦因数为0.152．
（2）小球下落的最大高度h为2.375m．
点评：本题考查了牛顿第二定律和运动学公式的综合，知道加速度是联系力学和运动学的桥梁．对于第一问，也可以对整体分析，运用牛顿第二定律进行求解．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
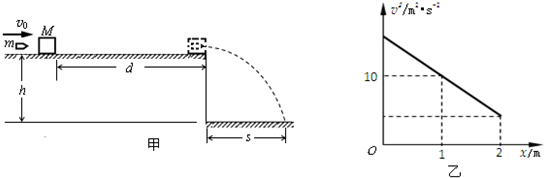如图甲所示，在高h=0.8m的平台上放置一质量为M=0.99kg的小木块（视为质点），小木块距平台右边缘d=2m，一质量m=0.01kg的子弹沿水平方向射入小木块并留在其中，然后一起向右运动，在平台上运动的v2-x关系如图乙所示．最后，小木块从平台边缘滑出落在距平台右侧水平距离s=0.8m的地面上，g取10m/s2，求：
