Question

【题目】如图所示，两个木块的质量分别为m1=2kg、m2=1kg，中间用轻弹簧相连接，放在光滑的水平面上，且m1左侧靠一固定竖直挡板，弹簧处于自然伸长状态．某一瞬间敲击木块m2使其获得3m/s的水平向左速度，木块m2向左压缩弹簧然后被弹簧弹回，弹回时带动木块m1运动．求：

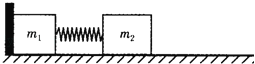
（1）当弹簧拉伸到最长时，弹簧的最大弹性势能是多少？

（2）在以后的运动过程中，木块m1速度的最大值为多少？

Answer 1

【答案】①当弹簧拉伸到最长时，弹簧的弹性势能为3J．

②在以后的运动过程中，木块m1速度的最大值为2m/s

【解析】解：①木块m2弹回后，在弹簧第一次恢复原长时带动m1运动，设此时木块m2的速度为v0，由机械能守恒定律可知：

v0=3m/s

当弹簧拉伸最长时，木块m1、m2速度相同，设为v，规定向左为正方向，由动量守恒定律得：m2v0=（m1+m2）v

解得：v=1m/s

由能量守恒定律可得弹簧的最大弹性势能Ep=m2v02﹣（m1+m2）v2=3J

②当弹簧再次恢复到原长时，m1获得最大速度为v1，此时m2的速度为v2

规定向右为正方向，由动量守恒定律得：m2v0=m1v1+m2v2

由机械能守恒定律得：m2v02=m1v12+m2v22

解得：v1=2m/s

答：①当弹簧拉伸到最长时，弹簧的弹性势能为3J．

②在以后的运动过程中，木块m1速度的最大值为2m/s．