题目内容
【题目】如图(a)所示为磁悬浮列车模型,质量M=1kg的绝缘板底座静止在动摩擦因数μ1=0.1的粗糙水平地面上.位于磁场中的正方形金属框ABCD为动力源,其质量m=1kg,边长为1m,电阻为![]() Ω.与绝缘板间的动摩擦因数μ2=0.4,OO′为AD、BC的中线.在金属框内有可随金属框同步移动的磁场,OO′CD区域内磁场如图(b)所示,CD恰在磁场边缘以外;OO′BA区域内磁场如图(c)所示,AB恰在磁场边缘以内(g=10m/s2).若绝缘板足够长且认为绝缘板与地面间最大静摩擦力等于滑动摩擦力.
Ω.与绝缘板间的动摩擦因数μ2=0.4,OO′为AD、BC的中线.在金属框内有可随金属框同步移动的磁场,OO′CD区域内磁场如图(b)所示,CD恰在磁场边缘以外;OO′BA区域内磁场如图(c)所示,AB恰在磁场边缘以内(g=10m/s2).若绝缘板足够长且认为绝缘板与地面间最大静摩擦力等于滑动摩擦力.
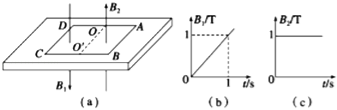
(1)若金属框固定在绝缘板上,则金属框从静止释放后,其整体加速度为多少?
(2)若金属框不固定,金属框的加速度又为多少?此时绝缘板是否静止,若不静止,其加速度又是多少?
【答案】(1)若金属框固定在绝缘板上,则金属框从静止释放后,其整体加速度为3 m/s2.
(2)若金属框不固定,金属框的加速度又为4 m/s2此时绝缘板不静止,其加速度又是2 m/s2
【解析】试题分析:(1)若金属框固定在绝缘板上,由题意得:
E=![]() SABCD=1××1×1 V="0.5" V,
SABCD=1××1×1 V="0.5" V,
则电流为:I=="8" A,
那么安培力为:FAB=B2IL="8" N,
取绝缘板和金属框整体进行受力分析,由牛顿第二定律有:
FAB﹣μ1(M+m)g=(M+m)a,
解得:a="3" m/s2.
(2)若金属框不固定,对金属框进行受力分析,假设其相对绝缘板滑动,有:
Ff1=μ2mg=0.4×1×10 N="4" N,
对金属框应用牛顿第二定律得:FAB﹣Ff1=ma1,a1="4" m/s2;
对绝缘板应用牛顿第二定律得:Ff1﹣Ff2=Ma2,Ff2=μ1(M+m)g="2" N,
解得:a2="2" m/s2,
a1>a2,假设正确.
金属框、绝缘板的加速度分别为4 m/s2、2 m/s2.

 阅读快车系列答案
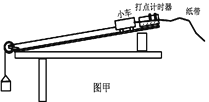
阅读快车系列答案【题目】小华所在的实验小组利用如图所示的实验装置探究牛顿第二定律,打点计时器使用的交流电频率f =50Hz,当地的重力加速度为g.
(1)在实验前必须进行平衡摩擦力,其步骤如下:取下细线和砂桶,把木板不带滑轮的一端适当垫高并反复调节,直到轻推小车,小车做_______________运动
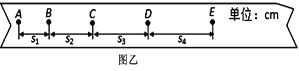
(2)图(乙)是小华同学在正确操作下获得的一条纸带,其中A、B、C、D、E每两点之间还有4个点没有标出.若s1=2.02cm,s2=4.00cm,s3=6.01cm,则B点的速度为:vB=_________m/s(保留三位有效数字)。
(3)在平衡好摩擦力的情况下,探究小车加速度a与小车质量M的关系中,某次实验测得的数据如表所示.根据这些数据在坐标图中描点并作出![]() 图线.从
图线.从![]() 图线求得合外力大小为______N(计算结果保留两位有效数字).
图线求得合外力大小为______N(计算结果保留两位有效数字).
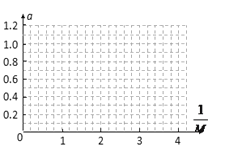
a/m·s-2 | 1.2 | 1.1 | 0.6 | 0.4 | 0.3 |
| 4.0 | 3.6 | 2.0 | 1.4 | 1.0 |
(4)如果在某次实验中根据测得的多组数据画出a-F关系图线如图所示。
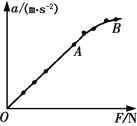
①分析此图线的OA段可得出的实验结论是 。
②此图线的AB段明显偏离直线,造成此误差的主要原因是
A.小车与轨道之间存在摩擦 B.轨道保持了水平状态
C.所挂砂及砂桶的总质量太大 D.所用小车的质量太大