题目内容
【题目】如图所示,将小球从斜面顶端A以速度v0=10m/s水平抛出,小球恰好落入斜面底端C处的接收盒中.已知斜面的直角边AB:BC=1:2,重力加速度大小g=10m/s2.
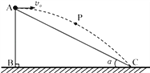
(1)求小球在空中飞行的时间;
(2)P点是小球运动轨迹上距离斜面最远的点,求小球经过P点的速度大小;
(3)求小球落到C点时的速度方向与水平面所夹的锐角.
【答案】(1)1s (2)![]() (3)
(3)![]()
【解析】试题分析:小球做的是平抛运动,研究平抛运动的方法是把平抛运动分解到水平方向和竖直方向去研究,水平方向做匀速直线运动,竖直方向做自由落体运动,两个方向上运动的时间相同,由此列式即可求解.当小球离斜面最远时,速度方向平行于斜面,将P点的速度分解为水平和竖直方向,根据几何关系即可求出P点的速度;求出小球到达C点时的竖直分速度,根据![]() 求出速度方向与水平面所夹的锐角。
求出速度方向与水平面所夹的锐角。
(1)设小球从A到C的时间为t,由平抛运动规律:
竖直方向:![]()
水平方向:![]()
联立已知条件解得:![]()
(2)设α为斜面与水平面的夹角:![]()
小球在P点的速度方向与斜面平行,则:![]()
联立解得:![]()
(3)小球落到C点时的竖直分速度:![]()
设β为小球落到C点时的速度方向与水平面所夹的锐角:![]()
联立解得:β=45°

练习册系列答案
相关题目