题目内容
【题目】如图所示,空间存在着一个范围足够大的竖直向下的匀强磁场,磁场的磁感强度大小为B;边长为L的正方形金属框abcd(简称方框)放在光滑的水平地面上,其外侧套着一个与方框边长相同的U型金属框架MNPQ(仅有MN、NQ、QP三条边,简称U型框),U型框的M、P端的两个触点与方框接触良好且无摩擦,其它地方没有接触。两个金属框每条边的质量均为m,每条边的电阻均为r。
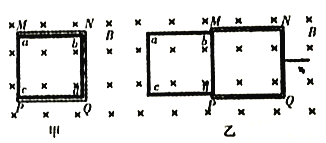
(1)若方框固定不动,U型框以速度v0垂直NQ边向右匀速运动,当U型框的接触点M、P端滑至方框的最右侧时,如图乙所示,求:U型框上N、Q两端的电势差UNQ;
(2)若方框不固定,给U型框垂直NQ边向右的水平初速度v0,U型框恰好不能与方框分离求:方框最后的速度v1和此过程流过U型框上NQ边的电量q;
(3)若方框不固定,给U型框垂直NQ边向右的初速度v(v>v0),在U型框与方框分离后,经过t时间,方框的最右侧和U型框的最左侧之间的距离为s。求:分离时U型框的速度大小v1和方框的速度大小v2。
【答案】(1) ![]() (2)
(2) ![]()
![]() (3)
(3) ![]()
![]()
【解析】
U型框向右做切割磁感线运动,由![]() 和由闭合电路欧姆定律求感应电流的大小和型框上N、Q两端的电势差;当U型框向右运动过程,方框和U型框组成系统合外力为零,系统动量守恒,根据动量守恒定律求出方框最后的速度;对U型框,由动量定理和电流概念求出此过程流过U型框上NQ边的电量;U型框和方框分离时系统动量守恒,根据题意列式求出分离时U型框的速度大小和方框的速度大小;
和由闭合电路欧姆定律求感应电流的大小和型框上N、Q两端的电势差;当U型框向右运动过程,方框和U型框组成系统合外力为零,系统动量守恒,根据动量守恒定律求出方框最后的速度;对U型框,由动量定理和电流概念求出此过程流过U型框上NQ边的电量;U型框和方框分离时系统动量守恒,根据题意列式求出分离时U型框的速度大小和方框的速度大小;
解:(1)由法拉第电磁感应定律得:![]()
此时电路图如图
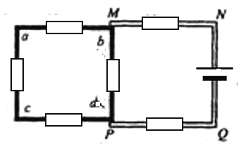
由串并联电路规律
外电阻为:![]()
由闭合电路欧姆定律得:
流过QN的电流:![]()
所以: ![]()
(2)当U型框向右运动过程,方框和U型框组成系统合外力为零,系统动量守恒
依题意得:方框和U型框最终速度相同,设最终速度大小为![]()
![]()
解得:![]()
对U型框,由动量定理得:![]()
由电流概念得:![]()
解得:![]()
(3)设:U型框和方框分离时速度分别为v1和v2
系统动量守恒:![]()
依题意得: ![]()
解方程可得:![]()
![]()

 阅读快车系列答案
阅读快车系列答案