题目内容
【题目】如图所示,光滑平行金属导轨与水平面间的夹角为θ,导轨电阻不计,下端与阻值为R的电阻相连。匀强磁场垂直导轨平面向上,磁感应强度大小为B。 一质量为m、长为L、电阻为r的导体棒垂直导轨放置,从ab位置以初速度v沿导轨向上运动,刚好能滑行到与ab相距为s的a′b′位置,然后再返回到ab。该运动过程中导体棒始终与导轨保持良好接触,不计空气阻力,重力加速度为g。下列说法正确的是( )
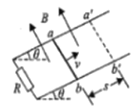
A.向上滑行过程中导体棒做匀减速直线运动
B.上滑过程中电阻R产生的热量为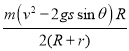
C.向下滑行过程中通过电阻R的电荷量为![]()
D.电阻R在导体榛向上滑行过程中产生的热量小于向下滑行过程中产生的热量
【答案】BC
【解析】
向上滑行过程中导体棒受到重力、安培力,根据牛顿第二定律分析加速度的变化情况;上滑过程中根据功能关系结合焦耳定律求解电阻R产生的热量;根据电荷量的计算公式求解向下滑行过程中通过电阻R的电荷量;根据![]() 分析电阻R在导体棒向上滑行过程中产生的热量与向下滑行过程中产生的热量的大小。
分析电阻R在导体棒向上滑行过程中产生的热量与向下滑行过程中产生的热量的大小。
A.向上滑行过程中导体棒受到重力、安培力,根据右手定则可得棒中的电流方向![]() ,根据左手定则可得安培力方向沿斜面向下,根据牛顿第二定律可得:
,根据左手定则可得安培力方向沿斜面向下,根据牛顿第二定律可得:
![]()
其中:
![]()
解得:
![]()
由于速度减小,则加速度减小,棒不做匀减速直线运动,故A错误;
B.设上滑过程中克服安培力做的功为W,根据功能关系可得:
![]()
克服安培力做的功等于产生的焦耳热,则:
![]()
上滑过程中电阻R产生的热量为:
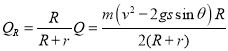
故B正确;
C.向下滑行过程中通过电阻R的电荷量为:
![]()
故C正确;
D.由于上滑过程中和下滑过程中导体棒通过的位移相等,即导体棒扫过的面积S相等,根据安培力做功计算公式可得:
![]()
由于上滑过程中的平均速度大于,下滑过程中的平均速度,所以上滑过程中平均电流大于下滑过程中的平均电流,则电阻R在导体棒向上滑行过程中产生的热量大于向下滑行过程中产生的热量,故D错误。
故选BC。