题目内容
15. 如图所示,一束电子经加速电场加速后进入偏转电场,已知电子的电荷量为e,质量为m,加速电场的电压为U1,偏转电场两极板间的距离为d,极板长度为L.问:
如图所示,一束电子经加速电场加速后进入偏转电场,已知电子的电荷量为e,质量为m,加速电场的电压为U1,偏转电场两极板间的距离为d,极板长度为L.问:(1)电子进入偏转电场时的速度大小;
(2)若要使得电子在飞出偏转电场时的侧位移恰好为$\frac{3d}{4}$,则需在偏转电场两极板间加上多大电压.
分析 (1)根据动能定理即可求得电子进入偏转电场时的速度大小;
(2)电子进入偏转电场后,做类平抛运动,根据水平方向做匀速直线运动,竖直方向做匀加速直线运动,即可求解
解答 解:(1)由动能定理可得:eU1=$\frac{1}{2}{mv}_{0}^{2}$
${v}_{0}=\sqrt{\frac{2e{U}_{1}}{m}}$
(2)电子进入偏转电场后,做类平抛运动
竖直方向:$\frac{3d}{4}=\frac{1}{2}a{t}^{2}$
水平方向:$t=\frac{L}{{v}_{0}}$
电子的加速度:$a=\frac{F}{m}=\frac{eU}{md}$
得:$U=\frac{3{U}_{1}{d}^{2}}{{L}^{2}}$
答:(1)电子进入偏转电场时的速度大小为$\sqrt{\frac{2e{U}_{1}}{m}}$;
(2)若要使得电子在飞出偏转电场时的侧位移恰好为$\frac{d}{2}$,则在偏转电场两极板间加的电压为$\frac{3{U}_{1}{d}^{2}}{{L}^{2}}$
点评 本题关键是将电子的类似平抛运动沿着平行初速度方向和垂直初速度方向进行正交分解,然后根据运动学规律、牛顿第二定律和电势差与场强的关系公式列式求解

练习册系列答案
相关题目
5.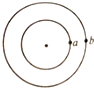 如图是我国北斗导航系统的两颗a、b,两卫星在同一平面内绕地球做匀速圆周运动,下列说法正确的是( )
如图是我国北斗导航系统的两颗a、b,两卫星在同一平面内绕地球做匀速圆周运动,下列说法正确的是( )
 如图是我国北斗导航系统的两颗a、b,两卫星在同一平面内绕地球做匀速圆周运动,下列说法正确的是( )
如图是我国北斗导航系统的两颗a、b,两卫星在同一平面内绕地球做匀速圆周运动,下列说法正确的是( )| A. | a卫星的运行速度小于b卫星的运行速度 | |
| B. | a卫星的运行速度大于b卫星的运行速度 | |
| C. | a卫星的运行周期大于b卫星的运行周期 | |
| D. | a卫星的运行角速度小于b卫星的运行的运行角速度 |
6. 如图所示,质量为m的滑块A受到与水平方向成θ角斜向上方的拉力F作用,向右做匀速直线运动,则滑块受到的拉力与摩擦力的合力的大小和方向是( )
如图所示,质量为m的滑块A受到与水平方向成θ角斜向上方的拉力F作用,向右做匀速直线运动,则滑块受到的拉力与摩擦力的合力的大小和方向是( )
 如图所示,质量为m的滑块A受到与水平方向成θ角斜向上方的拉力F作用,向右做匀速直线运动,则滑块受到的拉力与摩擦力的合力的大小和方向是( )
如图所示,质量为m的滑块A受到与水平方向成θ角斜向上方的拉力F作用,向右做匀速直线运动,则滑块受到的拉力与摩擦力的合力的大小和方向是( )| A. | Fsin θ | B. | mg-Fsin θ | C. | 竖直向上 | D. | 向上偏右 |
3. 如图,将小球从距斜轨底面h高处由静止释放,使其沿竖直的半径为R的圆形轨道的内侧运动.不计一切摩擦阻力,下列说法中正确的是( )
如图,将小球从距斜轨底面h高处由静止释放,使其沿竖直的半径为R的圆形轨道的内侧运动.不计一切摩擦阻力,下列说法中正确的是( )
 如图,将小球从距斜轨底面h高处由静止释放,使其沿竖直的半径为R的圆形轨道的内侧运动.不计一切摩擦阻力,下列说法中正确的是( )
如图,将小球从距斜轨底面h高处由静止释放,使其沿竖直的半径为R的圆形轨道的内侧运动.不计一切摩擦阻力,下列说法中正确的是( )| A. | 若h=R,那么小球不能到达与圆心O等高的C点 | |
| B. | 若h=2R,那么小球刚好能通过最高点D | |
| C. | 若h=3R,小球一定通过最高点D | |
| D. | 若h=4R,小球通过最高点D时,对轨道压力的大小是小球重力的4倍 |
4.下列关于电场的描述,正确的是( )
| A. | 电场中某点电势的大小、正负与零电势点的选取有关 | |
| B. | 电场中某两点间的电势差与零电势点的选取有关 | |
| C. | 同一点电荷处于电场中的不同位置时,具有的电势能越大,说明那一点的电势越高 | |
| D. | 同一点电荷在电场中任意两点间移动时,只要静电力做的功相同,那么两点间的电势差一定相同 |




 如图,传送带与水平地面的倾角θ=37°,A、B两端相距5.0m,一物体以v0=6.0m/s的初速度从A端冲上传送带,物体与传送带间的动摩擦因为0.5.传送带顺时针运转且速度v=4.0m/s,(g取10m/s2,sin37°=0.6,cos37°=0.8)求:
如图,传送带与水平地面的倾角θ=37°,A、B两端相距5.0m,一物体以v0=6.0m/s的初速度从A端冲上传送带,物体与传送带间的动摩擦因为0.5.传送带顺时针运转且速度v=4.0m/s,(g取10m/s2,sin37°=0.6,cos37°=0.8)求: