题目内容
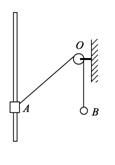
(12分)如图所示,质量为M、内有半径R的半圆形轨道的槽体放在光滑的平台上,左端紧靠一台阶,质量为m的小物体从A点由静止释放,若槽内光滑。 求:
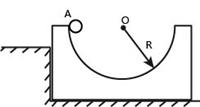
(1)小物体滑到圆弧最低点时的速度大小v
(2)小物体滑到圆弧最低点时,槽体对其支持力N的大小
(3)小物体上升的最大高度h

(1)小物体滑到圆弧最低点时的速度大小v
(2)小物体滑到圆弧最低点时,槽体对其支持力N的大小
(3)小物体上升的最大高度h
(1) ;(2)
;(2)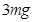 ;(3)
;(3)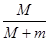 R
R
 ;(2)
;(2)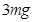 ;(3)
;(3)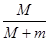 R
R试题分析:(1)设小物体由A落至圆弧最低点时的速度为v,取圆弧最低点为势能零点,
由机械能守恒定律得:mgR=
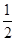 mv2 2分
mv2 2分得v=
 1分
1分(2)在最低点对小球受力分析,由
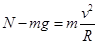 得: 2分
得: 2分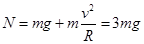 1分
1分(3)小物体向上运动的过程中,m与M组成的系统在水平方向的动量守恒:
设小球滑至最高点时m与M的共同速度为v′
所以 mv=(M+m)v′ 2分
解得:v′=
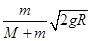 1分
1分此过程中系统机械能守恒,所以
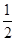 mv2-
mv2-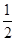 (M+m)v′2=mgh 2分
(M+m)v′2=mgh 2分解得m上升的最大高度h=
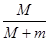 R. 1分
R. 1分
练习册系列答案
相关题目
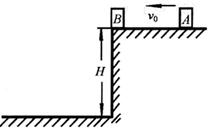
 .
.
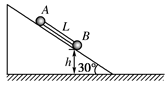
 的初动能从倾角为
的初动能从倾角为 的斜面顶端水平抛出,不计空气阻力。当它下落到斜面上时,小球的动能为
的斜面顶端水平抛出,不计空气阻力。当它下落到斜面上时,小球的动能为 ;在此过程中小球的重力势能减少了
;在此过程中小球的重力势能减少了
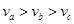
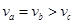
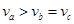
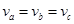
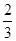 J
J