题目内容
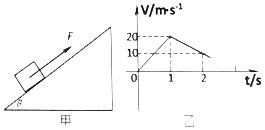
【题目】如图所示,半径为R的圆管BCD竖直放置,一可视为质点的质量为m的小球以某一初速度从A点水平抛出,恰好从B点沿切线方向进入圆管,到达圆管最高点D后水平射出.已知小球在D点对管下壁压力大小为![]() mg,且A、D两点在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力.求:
mg,且A、D两点在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力.求:

(1)小球在A点初速度的大小;
(2)小球在D点角速度的大小;
(3)小球在圆管内运动过程中克服阻力做的功.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据几何关系求出平抛运动下降的高度,从而求出竖直方向上的分速度,根据运动的合成和分解求出初速度的大小.
(2)根据向心力公式求出小球在D点的速度,从而求解小球在D点角速度.
(3)对A到D全程运用动能定理,求出小球在圆管中运动时克服阻力做的功.
(1)小球从A到B,竖直方向: vy2=2gR(1+cos 60°)
解得vy=![]()
在B点:v0=![]() =
=![]() .
.
(2)在D点,由向心力公式得mg-![]() mg=
mg=![]()
解得vD=![]()
ω=![]() =
=![]() .
.
(3)从A到D全过程由动能定理:-W克=![]() mvD2-
mvD2-![]() mv02
mv02
解得W克=![]() mgR.
mgR.

练习册系列答案
相关题目