题目内容
【题目】质量不等的两星体在相互间的万有引力作用下，绕两者连线上某一定点O做匀速圆周运动，构成双星系统．由天文观察测得其运动周期为
，两星体之间的距离为
，已知引力常量为
．下列说法正确的是
A．双星系统的平均密度为
B．O点离质量较大的星体较远
C．双星系统的总质量为
D．若在O点放一物体，则物体受两星体的万有引力合力为零
【答案】C
【解析】
试题分析：双星做圆周运动的角速度大小相等，靠相互间的万有引力提供向心力，知向心力大小相等，则有：
，则
，因为两颗恒星的质量不等，则做圆周运动的半径不同；双星中质量较大的轨道半径小，O点离质量较大的星体较近，故B错误．根据
，
，联立两式解得：
，故C正确．双星系统的平均密度为
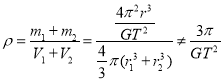，故A错误．因为O点离质量较大的星体较近，根据万有引力定律可知若在O点放一物体，则物体受质量大的星体的万有引力较大，故合力不为零．故D错误．故选C．
练习册系列答案
阅读快车系列答案
相关题目
