题目内容
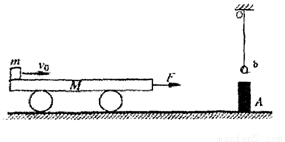
如图所示,质量M=3kg且足够长的木板放在水平光滑的平面上,在水平恒力F=11N作用下由静止开始向右运动,当速度达到1m/s时,将质量m=4kg的物块轻轻放到木板的右端,已知物块与木板间摩擦因数μ=0.2,(g=10m/s2),求:(1)物块经多长时间才与木板保持相对静止;
(2)物块与木板相对静止后,物块受到的摩擦力多大?
(3)全过程产生的热量是多少?

【答案】分析:(1)物体与木板均做匀变速直线运动,由牛顿第二定律可求得二者的加速度,由速度公式可求得二者相对静止的时间;
(2)相对静止后,物体的静摩擦力充当向心力,由牛顿第二定律可求得物体受到的摩擦力.
(3)通过运动学公式求出物块与木板之间的相对路程,从而求出全过程中产生的热量.
解答:解:(1)放上物体后,由牛顿第二定律可知:
物体加速度 a1=μg=2m/s2
板的加速度 a2=
当两物体达速度相等后保持相对静止,故a1t=v+a2t
∴t=1s
(2)相对静止后,对整体 F=(M+m)a
对物体有f=ma
解得f=6.28N
(3)1s内物块的位移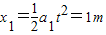 ,木板的位移
,木板的位移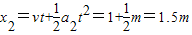 .
.
则相对路程△x=0.5m
则全过程产生的热量Q=f△x=μmg△x=4J.
答:(1)物块经1s时间才与木板保持相对静止;
(2)物块与木板相对静止后,物块受到的摩擦力为6.28N.
(3)全过程产生的热量是4J.
点评:解决本题的关键理清物块和木板的运动过程,结合牛顿第二定律和运动学公式进行求解.
(2)相对静止后,物体的静摩擦力充当向心力,由牛顿第二定律可求得物体受到的摩擦力.
(3)通过运动学公式求出物块与木板之间的相对路程,从而求出全过程中产生的热量.
解答:解:(1)放上物体后,由牛顿第二定律可知:
物体加速度 a1=μg=2m/s2
板的加速度 a2=

当两物体达速度相等后保持相对静止,故a1t=v+a2t
∴t=1s
(2)相对静止后,对整体 F=(M+m)a
对物体有f=ma
解得f=6.28N
(3)1s内物块的位移
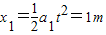 ,木板的位移
,木板的位移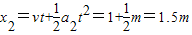 .
.则相对路程△x=0.5m
则全过程产生的热量Q=f△x=μmg△x=4J.
答:(1)物块经1s时间才与木板保持相对静止;
(2)物块与木板相对静止后,物块受到的摩擦力为6.28N.
(3)全过程产生的热量是4J.
点评:解决本题的关键理清物块和木板的运动过程,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
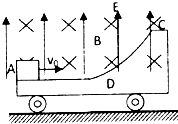 如图所示,质量M=3.0kg的小车静止在光滑的水平面上,AD部分是表面粗糙的水平导轨,DC部分是光滑的l/4圆弧导轨,整个导轨都是由绝缘材料制成的,小车所在平面内有竖直向上E=40N/C的匀强电场和垂直纸面向里B=2.0T的匀强磁场.今有一质量为m=1.0kg带负电的滑块(可视为质点)以v0=8m/s的水平速度向右冲上小车,当它即将过D点时速度达到v1=5m/s,对水平导软的压力为l0.5N,(g取10m/s2).
如图所示,质量M=3.0kg的小车静止在光滑的水平面上,AD部分是表面粗糙的水平导轨,DC部分是光滑的l/4圆弧导轨,整个导轨都是由绝缘材料制成的,小车所在平面内有竖直向上E=40N/C的匀强电场和垂直纸面向里B=2.0T的匀强磁场.今有一质量为m=1.0kg带负电的滑块(可视为质点)以v0=8m/s的水平速度向右冲上小车,当它即将过D点时速度达到v1=5m/s,对水平导软的压力为l0.5N,(g取10m/s2). ,g取10m/s2。
,g取10m/s2。

 ,g取10m/s2。
,g取10m/s2。
