题目内容
如图所示，质量M=3.0kg的小车静止在光滑的水平地面上，其右侧足够远处有一挡板A，质量m=2.0kg的b球用长l=2m的细线悬挂于挡板正上方。一质量也为m＝2kg的滑块(视为质点)，以υ0=7m/s的初速度从左端滑上小车，同时对小车施加水平向右、大小为6N的恒力F，当滑块运动到平板车的最右端时，二者恰好相对静止，此时撤去恒力F。平板车碰到挡板时立即停止运动，滑块水平飞出小车后与b球正碰并粘在一起。已知滑块与小车间的动摩擦因数μ=0.3，g=10m/s2，问：
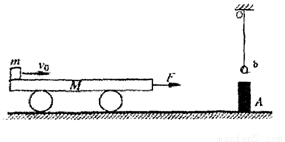
（1）撤去恒力F前，滑块、小车的加速度各为多大，方向如何?
（2）撤去恒力F时，滑块的速度为多大？
（3）悬挂b球的细线能承受的最大拉力为30N，a、b两球碰后，细线是否会断裂?(要求通过计算回答)
【答案】
（1）a2=4m/s2，方向水平向右（2）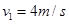
（3）细线会断裂
【解析】
试题分析：（1）由牛顿第二定律得：
对滑块：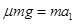
(2分)
解得：a1=3m/s2(1分)，方向水平向左(1分)
对平板车：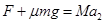
(2分)
a2=4m/s2(1分)，方向水平向右(1分)
（2）设经过时间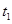
滑块与平板车相对静止，此时撤去恒力F，滑块的速度为
，
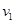则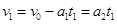
解得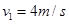
（3）滑块与小球碰撞，动量守恒，故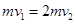
设细线的拉力为T，根据牛顿第二定律可得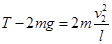
代入数据可得：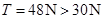
，故细线会断裂
考点：考查了牛顿第二定律，运动学公式，动量守恒定律的综合应用，难度一般
练习册系列答案
相关题目
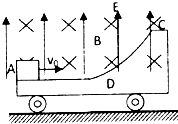如图所示，质量M=3.0kg的小车静止在光滑的水平面上，AD部分是表面粗糙的水平导轨，DC部分是光滑的l/4圆弧导轨，整个导轨都是由绝缘材料制成的，小车所在平面内有竖直向上E=40N/C的匀强电场和垂直纸面向里B=2.0T的匀强磁场．今有一质量为m=1.0kg带负电的滑块（可视为质点）以v0=8m/s的水平速度向右冲上小车，当它即将过D点时速度达到v1=5m/s，对水平导软的压力为l0.5N，（g取10m/s2）．
，g取10m/s2。
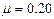，g取10m/s2。
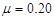，g取10m/s2。
