题目内容
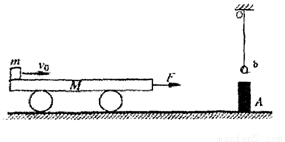
如图所示，质量M=3.0kg的平板小车静止在光滑水平面上，当t=0时，两个质量均为m=1.0kg的小物体A和B（均可视为质点），分别从左端和右端以水平速度v1=4.0m/s和v2=2.0m/s冲上小车，当它们在车上停止滑动时，A、B没有相碰。A、B与车面的动摩擦因数均为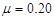
，g取10m/s2。
1.求A、B在车上停止滑动时车的速度；
2.车的长度至少是多少；
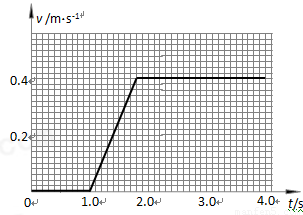
3.在图所给出的坐标系中画出0至4.0s内小车的速度—时间图象。
1.0.40m/s方向水平向右
2.4.8m
3.
【解析】（1）设A、B在车上停止滑动时，车的速度为v，根据动量守恒定律有：
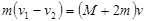……………………………………………………………………（2分）
解得 v = 0.40m/s……………………………………………………………………（1分）
方向水平向右。…………………………………………………………………………（1分）
（2）设A、B在车上相对于车滑动的距离分别为l1和l2，由功能关系有：
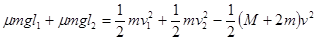……………………………（2分）
解得： l1+l2=4.8m，即车长至少为4.8m。………………………………………………（2分）
（3）车的运动分以下三个阶段：
第一阶段：A、B同时在车上滑行时，滑块对车的摩擦力均为μmg，方向相反，车受力平衡而保持不动。当B的速度减为0时，此过程结束。设这段时间内滑块的加速度为a，根据牛顿第二定律有：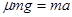
，解得滑块的加速度
。
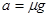滑块B在小车上相对滑行的时间为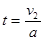 
＝1.0s。…………………………（1分）
第二阶段：B停止运动后，A继续在车上滑行，设到t2时刻物体A与车有共同速度v，则 v=v1-at2，
解得：t2=1.8s。…………………（1分）
第三阶段：t2之后，车以速度v做匀速直线运动。到t=4.0s为止，物体的速度时间图线如图答所示。………………（2分）
阳光课堂课时作业系列答案
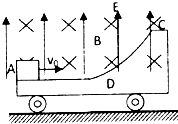如图所示，质量M=3.0kg的小车静止在光滑的水平面上，AD部分是表面粗糙的水平导轨，DC部分是光滑的l/4圆弧导轨，整个导轨都是由绝缘材料制成的，小车所在平面内有竖直向上E=40N/C的匀强电场和垂直纸面向里B=2.0T的匀强磁场．今有一质量为m=1.0kg带负电的滑块（可视为质点）以v0=8m/s的水平速度向右冲上小车，当它即将过D点时速度达到v1=5m/s，对水平导软的压力为l0.5N，（g取10m/s2）．
，g取10m/s2。
，g取10m/s2。
