Question

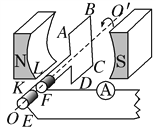
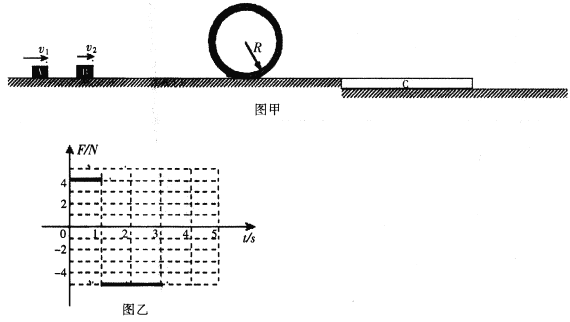
【题目】如图甲所示，一个光滑的水平平台，平台右边固定一个半径为1.28m，底端开口的光滑竖直圆形轨道，紧挨平台右侧有一个长木板C静置在光滑的水平面上，木板上表面和平台等高。有两个可视为质点、质量分别为和的滑块A和B，在平台上分别以速度和向右运动，且>，在进入圆形轨道前，两滑块相碰。

(1)请应用牛顿运动定律推导出A和B碰撞过程中动量守恒定律的表达式，要求说明推导过程中每步的根据，以及式中各符号和最后结果中各项的意义。

(2)如果滑块A和B碰撞结束后，搬走A，B恰好通过竖直圆形轨道后滑上长木板C，B与C间动摩擦因数为0.2.老质量均为1kg，则C板的长度满足什么条件，B才不会从C上掉下来?

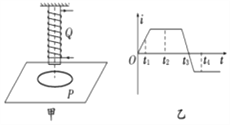
(3)如果C板足够长，B以(2)中条件滑上C的同时，对C施加一个如图乙随时间变化的力(向右为正方向，3s末撤销该力)，求B最终在C上滑过的距离?

Answer 1

【答案】(1)略（2）C板的长度满足不小于8m，B才不会从C上掉下来（3）6.5m

【解析】解：（1）令F1和F2分别表示滑块A和B相互作用力，a1和a2分别表示它们的加速度，表示F1和F2作用的时间。v1' 和v2' 分别表示它们相互作用过程的末速度，根据牛顿第二定律，有

由于极短，由加速度的定义可知

代入上式，可得

根据牛顿第三定律，

整理以上两式得

其中为两滑块的初动量， 为两滑块的末动量，这就是动量守恒定律的表达式．

（2）B恰好通过竖直圆轨道，最高点速度为vm ，则

B滑上C时速度为vB 则有

解得

B滑上C到恰好与C共速过程

解得 L=8m

C板的长度满足不小于8m，B才不会从C上掉下来

（3）B滑上C后减速，加速度

C加速，加速度

设经时间t1共速，

解得 t1=1s

此时B、C速度

此后B减速加速度，C减速加速度

故C减速至0时间

此后C以 向右加速，经时间t3再次与B共速

解得t3=0.5s

C在3.5s内位移为

B滑上C后3.5s内位移为

故B最终在C上滑行距离为