题目内容
用一根长1 m的轻质细绳将一幅质量为1 kg的画框对称悬挂在墙壁上.已知绳能承受的最大张力为10 N.为使绳不断裂,画框上两个挂钉的间距最大为(g取10 m/s2)( )
A. m m | B. m m | C. m m | D. m m |
A
解析试题分析:一个大小方向确定的力分解为两个等大的力时,合力在分力的角平分线上,且两分力的夹角越大,分力越大,因而当绳子拉力达到F=10N的时候,绳子间的张角最大,为120°,此时两个挂钉间的距离最大;画框受到重力和绳子的拉力,三个力为共点力,受力如图.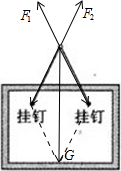
绳子与竖直方向的夹角为θ=60°,绳子长为L0=1m,则有mg=2Fcosθ,两个挂钉的间距离L=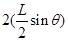 解得L=
解得L= m
m
考点:力的合成与分解的运用;共点力平衡的条件及其应用.

如图所示,重为100N的物体在水平面上向右运动,物体与水平面的动摩擦系数为0.2,与此同时物体受到一个水平向左的力F=20N,那么物体受到的合力为( )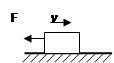
| A.0 | B.40N,水平向左; |
| C.20N,水平向右; | D.20N,水平向左 |
如图,质量为M的斜面静置在水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦.用恒力F沿斜面向上拉小物块,使之匀速上滑。在小物块运动的过程中,斜面始终保持静止.则( )
| A.地面对斜面的摩擦力大小为Fsinθ ,方向水平向右 |
| B.物块对斜面的摩擦力大小为F-mgcosθ,方向沿斜面向上 |
| C.地面对斜面的支持力大小为(M+m)g |
| D.地面对斜面的支持力为(M+m)g-Fsinθ |
如图所示,一小车的表面由一光滑水平面和光滑斜面连接而成,其上放一球,球与水平面的接触点为a,与斜面的接触点为b.当小车和球一起在水平桌面上做直线运动时,下列结论正确的是( )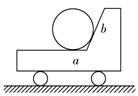
| A.球a、b两点处一定都受到支持力 |
| B.球在a点一定受到支持力,在b点处一定不受支持力 |
| C.球在a点一定受到支持力,在b点处不一定受到支持力 |
| D.球在a点处不一定受到支持力,在b点处也不一定受到支持力 |
同一平面内的两个共点力大小分别为4N和7N,则这两个力合力的可能值是( )
| A.3N | B.4N | C.11N | D.14N |
粗铁丝弯成如图所示半圆环的形状,圆心为O,半圆环最高点B处固定一个小滑轮,小圆环A用细绳吊着一个质量为m2的物块并套在半圆环上。一根一端拴着质量为m1的物块的细绳,跨过小滑轮后,另一端系在小圆环A上。设小圆环、滑轮、绳子的质量以及相互之间的摩擦均不计,绳子不可伸长。若整个系统平衡时角AOB为α,则两物块的质量比m1:m2为 
A.cos | B.2sin |
C.sin | D.2cos |
如图所示,绳与杆均不计重力,承受力的最大值一定.A端用绞链固定,滑轮O在A点正上方(滑轮大小及摩擦均可忽略),B端吊一重物P,现施加拉力FT将B缓慢上拉,在杆转到竖直前
| A.OB段绳中的张力变大 |
| B.OB段绳中的张力变小 |
| C.杆中的弹力大小不变 |
| D.杆中的弹力变大 |
 ,AO的拉力
,AO的拉力 和BO的拉力
和BO的拉力 的大小是( )
的大小是( )
 B.
B. C.
C.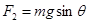 D.
D.

