题目内容
(15分)如图,在竖直平面内有一固定光滑轨道,其中AB是长为R的水平直轨道,BCD是圆心为O、半径为R的3/4圆弧轨道,两轨道相切与B点。在外力作用下,一小球从A点由静止开始做匀加速直线运动,到达B点时撤除外力。已知小球刚好能沿圆轨道经过最高点C,重力加速度大小为g。求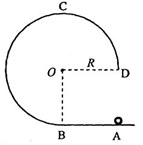
(1)小球在C点的速度的大小;
(2)小球在AB段运动的加速度的大小;
(3)小球从D点运动到A点所用的时间。
(1)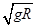 (2)
(2)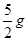 (3)
(3)
解析试题分析:(1)小球刚好能沿圆轨道经过最高点C,则有:
解得:
(2)在AB段:
在BC段,由动能定理,可得: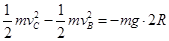
解得: ,
,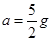
(3)在BC段,由动能定理,可得:
解得: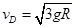
小球又回到A点时:
小球从D点运动到A点的时间:
考点:本题考查了竖直面内圆周运动的临界问题分析及动能定理的应用。

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
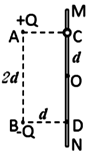
 ,P、Q两点的电势差为U,不计重力作用,求:
,P、Q两点的电势差为U,不计重力作用,求:




