题目内容
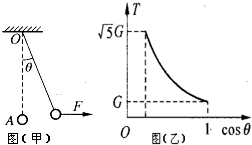
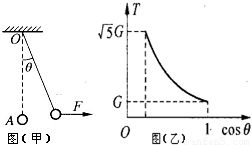
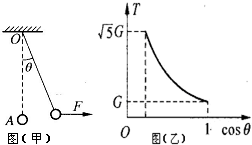 如(甲)所示,一根长为L的轻绳上端固定在O点,下端拴一个重为G的小钢球A,球处于静止状态.现对球施加一个方向水平向右的外力F,使球缓慢地偏移,在移动过程中的每一时刻,都可以认为球处于平衡状态,外力F方向始终水平向右,若轻绳上张力T的大小随轻绳与竖直方向的夹角θ的变化如图(乙)所示,求:
如(甲)所示,一根长为L的轻绳上端固定在O点,下端拴一个重为G的小钢球A,球处于静止状态.现对球施加一个方向水平向右的外力F,使球缓慢地偏移,在移动过程中的每一时刻,都可以认为球处于平衡状态,外力F方向始终水平向右,若轻绳上张力T的大小随轻绳与竖直方向的夹角θ的变化如图(乙)所示,求:(1)水平拉力F对应θ变化的取值范围.
(2)在上述过程中水平拉力F所做的功.
分析:(1)当cosθ=1时,即θ=0时,绳子拉力等于重力,水平拉力等于0.根据共点力平衡求出拉力为
G时,水平拉力的大小,从而得出拉力的范围.
(2)因为缓慢移动,动能变化为零,拉力做功等于重力势能的增加量.
| 5 |
(2)因为缓慢移动,动能变化为零,拉力做功等于重力势能的增加量.
解答:解:(1)当T=G时,F=0
当T=
G时,F=
=2G.
所以F的取值范围是0≤F≤2G.
(2)当F=2G时,cosθ=
,由功能关系得:
F做功W=GL(1-cosθ)=(
)GL.
答:(1)水平拉力F对应θ变化的取值范围0≤F≤2G.
(2)在上述过程中水平拉力F所做的功为(
)GL.
当T=
| 5 |
| T2-G2 |
所以F的取值范围是0≤F≤2G.
(2)当F=2G时,cosθ=
| ||
| 5 |
F做功W=GL(1-cosθ)=(
5-
| ||
| 5 |
答:(1)水平拉力F对应θ变化的取值范围0≤F≤2G.
(2)在上述过程中水平拉力F所做的功为(
5-
| ||
| 5 |
点评:本题考查了共点力平衡,以及功能关系,难度不大,是一道好题,平时需加强这方面的训练.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端
如图所示,一根长为L、质量为100kg的木头,其重心O在离粗端