Question

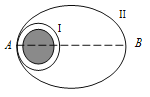
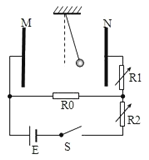
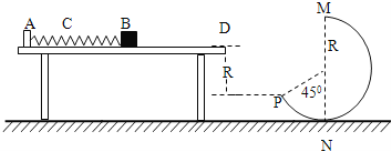
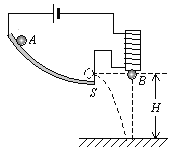
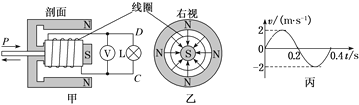
【题目】如图甲所示是某同学设计的一种振动发电装置的示意图，它的结构是一个套在辐向形永久磁铁槽中的半径为r＝0.1 m、匝数n＝100 的线圈，磁场的磁感线均沿半径方向均匀分布(其右视图如图乙所示)。线圈所在位置磁感应强度B的大小均为B＝T，线圈的电阻为R1＝0.5 Ω，它的引出线接有R2＝9.5 Ω的小电珠L。外力推动线圈框架的P端，使线圈沿轴线做往复运动，便有电流通过电珠。当线圈运动速度v随时间t变化的规律如图丙所示时(摩擦等损耗不计)，从t＝0时刻开始计时。

(1)写出线圈中产生的感应电动势的瞬时值表达式以及电压表中的示数；

(2)通电40 s小电珠L消耗的电能；

(3)t＝0.1 s时外力F的大小。

Answer 1

【答案】(1)e＝40sin 5πt(V) 38 V　(2)6080J (3)160 N

【解析】

(1)由题图丙可得：vm＝2 m/s，T＝0.4 s

电动势最大值

Em＝nBLvm＝nB·2πr·vm＝40V

线圈转动的角速度

ω＝＝5πrad/s

电动势的瞬时值表达式：

e＝40sin5πt(V)

电动势的有效值

E＝＝V＝40V

电流的有效值

I＝＝A＝4A

电压表的示数

U＝IR2＝4×9.5V＝38V

(2)根据焦耳定律可得：

Q＝I2R2t＝42×9.5×40J＝6 080J

(3)t＝0.1 s时e＝Em＝40 V

电流强度

i＝Im＝＝A＝4A

此时线圈的速度最大而加速度为零，则：

F＝FA＝nBIm·2πr＝100××4×2π×0.1N＝160N