题目内容
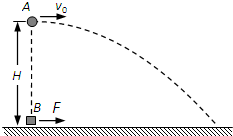 如图,在距地面高为H=45m处,某时刻将一小球A以初速度v0=10m/s水平向右抛出,与此同时,在A的正下方有一质量mB=1kg的物块B受水平向右恒力F=6N作用从静止开始运动,B与水平地面间的动摩擦因数μ=0.2,A、B均可视为质点,空气阻力不计,g取10m/s2,求:
如图,在距地面高为H=45m处,某时刻将一小球A以初速度v0=10m/s水平向右抛出,与此同时,在A的正下方有一质量mB=1kg的物块B受水平向右恒力F=6N作用从静止开始运动,B与水平地面间的动摩擦因数μ=0.2,A、B均可视为质点,空气阻力不计,g取10m/s2,求:(1)A球从抛出到落至地面所用的时间.
(2)A球落地时,A、B之间的距离.
分析:(1)平抛运动在竖直方向上做自由落体运动,根据H=
gt2求出A球抛出到落到地面所用的时间.
(2)根据牛顿第二定律求出B物体的加速度,然后通过运动学公式求出这段时间内位移,从而求出A、B间的距离.
| 1 |
| 2 |
(2)根据牛顿第二定律求出B物体的加速度,然后通过运动学公式求出这段时间内位移,从而求出A、B间的距离.
解答:解:(1)A球在竖直方向做自由落体运动
由H=
gtA2解得
A球落到地面所用的时间 tA=
s=3s①
故A球抛出到落到地面所用的时间为3s.
(2)物块B在地面做匀加速直线运动,设加速度为a
由牛顿第二定律有 F-μmBg=mBa ②
由运动学公式有SB=
atA2③
联立②③解得B的位移SB=18 m ④
A球在水平方向做匀速直线运动
则A的水平位移sA=v0tA=10×3m=30 m ⑤
sAB=sA-sB=30m-18m=12 m
故A、B之间的距离为12m.
由H=
| 1 |
| 2 |
A球落到地面所用的时间 tA=
|
故A球抛出到落到地面所用的时间为3s.
(2)物块B在地面做匀加速直线运动,设加速度为a
由牛顿第二定律有 F-μmBg=mBa ②
由运动学公式有SB=
| 1 |
| 2 |
联立②③解得B的位移SB=18 m ④
A球在水平方向做匀速直线运动
则A的水平位移sA=v0tA=10×3m=30 m ⑤
sAB=sA-sB=30m-18m=12 m
故A、B之间的距离为12m.
点评:解决本题的关键知道平抛运动的规律,以及知道加速度是联系力学和运动学的桥梁,通过加速度,可以根据力求运动,也可以根据运动求力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
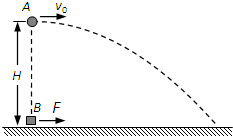
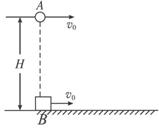

 如图,在距地面高为H=45m处,某时刻将一小球A以初速度v=10m/s水平向右抛出,与此同时,在A的正下方有一质量mB=1kg的物块B受水平向右恒力F=6N作用从静止开始运动,B与水平地面间的动摩擦因数μ=0.2,A、B均可视为质点,空气阻力不计,g取10m/s2,求:
如图,在距地面高为H=45m处,某时刻将一小球A以初速度v=10m/s水平向右抛出,与此同时,在A的正下方有一质量mB=1kg的物块B受水平向右恒力F=6N作用从静止开始运动,B与水平地面间的动摩擦因数μ=0.2,A、B均可视为质点,空气阻力不计,g取10m/s2,求: