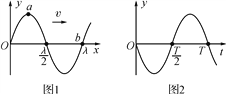题目内容
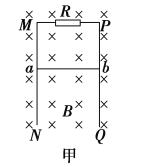
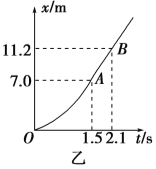
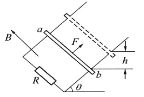
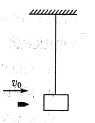
【题目】如图所示，M是水平放置的半径足够大的圆盘，绕过其圆心的数字轴匀速转动，规定经过同心O点且水平向右为x轴正方向，在O点正上方距盘面高h=2．5m处有一个可间断滴水的容器，从t=0时刻开始，容器沿水平轨道向X轴正方向做初速度为零的匀加速直线运动，已知t=0时刻滴下第一滴水，以后每当前一滴水刚好落到盘面时再滴下一滴水，取
（结果可用根式表示）
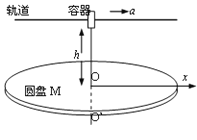
（1）求每一滴水从离开容器到滴落至盘面的时间t；
（2）要使每一滴水在盘面上的落点都位于同一直线上，求圆盘的角速度
应满足的条件；
（3）当圆盘的角速度
时，第二滴水与第三滴水在盘面上落点间的距离
，求容器的加速度a。
【答案】（1）
（2）
（n=1，2，3…）（3）
【解析】
试题分析：（1）离开容器后，每一滴水在竖直方向上做自由落体运动．
每一滴水滴落到盘面上所用时间
（2）要使每一滴水在盘面上的落点都位于同一直线，则圆盘在t秒内转过的弧度为
，n为不为零的正整数．所以
，即
，其中n=1，2，3…
（3）第二滴水离开O点的距离为
…①
第三滴水离开O点的距离为
…②
（上面①②两式中：
…③），
又
即第二滴水和第三滴水分别滴落在圆盘上x轴方向及垂直x轴的方向上．
所以
…④
联列①②③④可得：
．
练习册系列答案
相关题目
